Estimación de fase

La estimación de fase (EF) es una primitiva cuántica que es utilizada en distintos algoritmos. Permite extraer información legible de superposiciones.

Por ejemplo, es utilizada en el algoritmo de Shor, HHL, entre otros. Internamente, esta primitiva utiliza la transformada de Fourier inversa.

Objetivo

El objetivo de la primitiva es obtener una estimación de la fase global o autovalor (eigenvalue) de una operación aplicada a un estado cuántico que es autovector (eigenvector).

Para entender mejor qué valor es el que obtiene la primitiva se propone el siguiente ejemplo:

Supóngase el estado inicial $\ket{\psi}$ , el cual es un autovector de la operación $U$ . Al ser un autovector de $U$ , se cumple $U\ket{\psi}=e^{i \theta}\ket{\psi}$ , siendo $e^{i\theta}$ el autovalor.

Por ejemplo, suponiendo que existe un estado cuántico que es autovector de $U$ con el siguiente valor:

$$\ket{0}$$

$$\ket{1}$$

y que al aplicar la operación $U$ , se obtiene el siguiente estado:

$$\ket{0}$$

$$\ket{1}$$

$\overset{U}{\rightarrow}$

$$\ket{0}$$

$$\ket{1}$$

Notar que las magnitudes no cambiaron, ni la fase relativa cambió, y por ende se obtuvo el mismo estado cuántico pero con un autovalor $e^{\pi i}$ ( $180^\circ$ ).

El algoritmo de EF nos permite obtener una estimación sobre este autovalor.

Aunque parezca que esta información obtenida es arbitraria y que no sea practicamente útil, es altamente importante en muchos algoritmos como los mencionados previamente.

Solución

El algoritmo de estimación de fase se puede dividir en cuatro secciones: inicialización, superposición, aplicación de puertas controladas y uso de la transformada de Fourier cuántica inversa.

En el siguiente gráfico se dividen las etapas utilizando $\ket{\sigma_i}$ para representar el estado cuántico en cada sección.

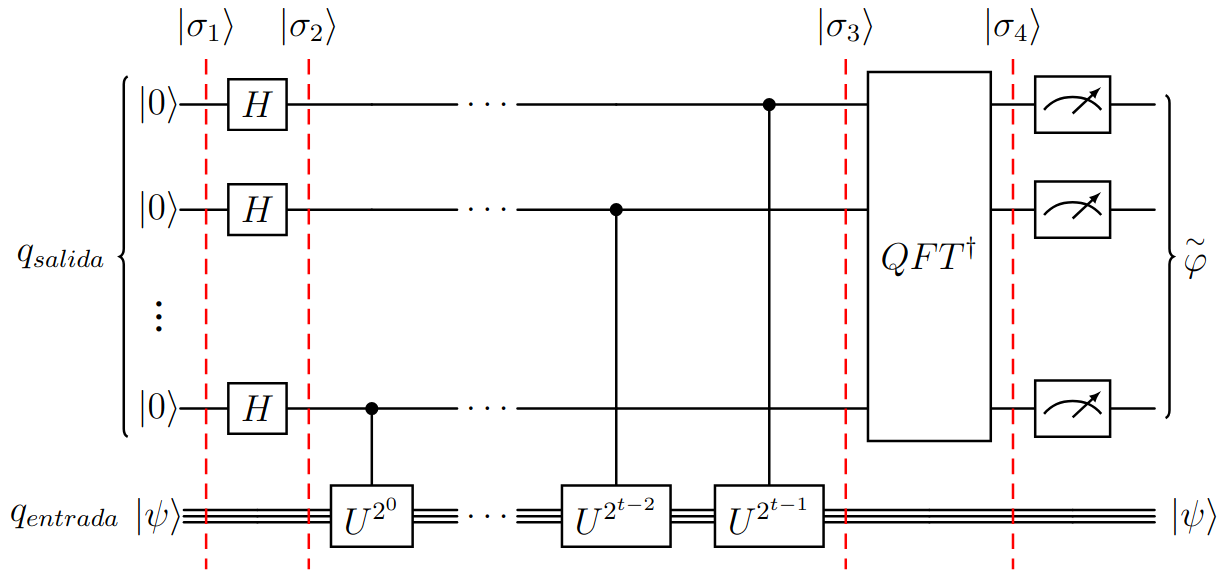
Estructura de la primitiva EF de forma general, con cuatro señalizadores indicando las distintas secciones del algoritmo. Las puertas siguen un patron escalonado del cubit de control, empezando por el ultimo (de arriba hacia abajo) y finalizando con el primero (el de arriba) como cubit de control.

Figura (1): Estructura de la primitiva EF de forma general, con cuatro señalizadores indicando las distintas secciones del algoritmo. En ciertas bibliografías se aplican las puertas U controladas con el orden inverso.

El algoritmo recibe tres parámetros como entrada:

$q_{salida}$ el cual es un registro inicializado en $0$ sobre el cual se dejará el resultado. Llamaremos $t$ al tamaño en cubits de $q_{salida}$ .
$q_{entrada}$ es el autovector del cual se quiere obtener el autovalor.
La puerta controlada de U.

La notación $U^{2^g}$ implica que se realizan $2^g$ operaciones sucesivas de U. Esto conlleva un gran costo computacional, por lo que se busca poder crear una puerta que cumpla el mismo funcionamiento que $U^{2^g}$ de una forma más eficiente que simplemente repetir la operación original.

En la primer etapa $\ket{\sigma_1}$ se inicializan los estados cuánticos, el registro de $q_{salida}$ con 0 y el registro $q_{entrada}$ con el autovector.

\begin{align} \ket{\sigma_1}&=\ket{0}^{\otimes t}\ket{\psi} \end{align}

Luego en la segunda etapa se crea una superposición de $q_{salida}$ :

\begin{align} \ket{\sigma_2}&=H^{\otimes t}\ket{0}^{\otimes t}\ket{\psi}\\ &=2^{-t/2}(\ket{0}+\ket{1})^{\otimes t}\ket{\psi}\\ &=2^{-t/2}(\ket{0}+\ket{1})(\ket{0}+\ket{1})\ldots(\ket{0}+\ket{1})\ket{\psi} \end{align}

En la tercer etapa se aplican las puertas controladas de U. Así, ocurre el fenómeno de retroceso de fase, por lo que aplicar la puerta $U^{2^h}$ puede generalizarse de la siguiente manera:

\begin{align} U^{2^h}\ket{\gamma}&=U^{2^{h-1}}U\ket{\gamma}\\ &=U^{2^{h-1}}e^{i \theta}\ket{\gamma}\\ &=e^{i\theta 2^{h}}\ket{\gamma} \end{align}

Por lo tanto, al aplicar las puertas controladas de U al estado superpuesto de $\ket{\sigma_2}$ se obtiene:

\begin{align} \ket{\sigma_3}&=2^{-t/2}(\ket{0}+e^{i \theta 2^{t}}\ket{1})(\ket{0}+e^{i \theta 2^{t-1}}\ket{1})\ldots(\ket{0}+e^{i \theta 2^{0}}\ket{1})\ket{\psi} \end{align}

Es útil reescribir $\theta=2\pi j$ , donde $j=0.j_{t-1}j_{t-2}\ldots j_0$ siendo $j$ una fracción en binario, para obtener un formato similar al de $QFT$ :

\begin{align} \ket{\sigma_3}&=2^{-t/2}(\ket{0}+e^{2\pi i 2^{t}(0.j_{t-1}j_{t-2}\ldots j_0)}\ket{1})(\ket{0}+e^{2\pi i 2^{t-1}(0.j_{t-1}j_{t-2}\ldots j_0) }\ket{1})\\& \ldots(\ket{0}+e^{2\pi i 2^{0}(0.j_{t-1}j_{t-2}\ldots j_0)}\ket{1})\ket{\psi} \end{align}

Aplicar la operación $2^h(0.j_{t-1}j_{t-2}\ldots j_0)$ implica realizar un desplazamiento binario (shift) de $h$ posiciones.

Hacer un desplazamiento a una fracción binaria puede incrementar la parte entera del número. Por ejemplo, si se desplaza la fracción binaria $0.11$ ( $0.75$ en decimal) por una posición se obtiene $1.10$ ( $2.5$ en decimal).

Debido a que multiplicar enteros por $2\pi$ es redundante, se puede simplificar de la siguiente manera:

\begin{align} \ket{\sigma_3}&=2^{-t/2}(\ket{0}+e^{2\pi i (0.j_0)}\ket{1})(\ket{0}+e^{2\pi i (0.j_1j_0) }\ket{1})\\& \ldots(\ket{0}+e^{2\pi i (0.j_{t-1}j_{t-2}\ldots j_0)}\ket{1})\ket{\psi} \end{align}

El resultado de esta simplificación es idéntico al estado cuántico luego de aplicar $QFT$ sobre el estado $\ket{j}$ . Por lo que aplicar $QFT^\dag$ resulta en $\ket{j}$ :

\begin{align} \ket{\sigma_4}&=QFT^\dag(2^{-t/2}(\ket{0}+e^{2\pi i (0.j_0)}\ket{1})(\ket{0}+e^{2\pi i (0.j_1j_0) }\ket{1})\\& \ldots(\ket{0}+e^{2\pi i (0.j_{t-1}j_{t-2}\ldots j_0)}\ket{1})\ket{\psi})\\ &=\ket{j} \end{align}

Finalmente, al medir la respuesta se obtiene una estimación de $j$ . A partir de $j$ se puede obtener el ángulo $\theta$ y su autovalor:

\begin{align} \theta&=2\pi j=2\pi0.j_{t-1}j_{t-2}\ldots j_0\\ autovalor &= e^{i \theta} \end{align}

Ejemplos

Para este ejemplo se utilizará la operación Hadamard con su versión controlada.

El autovector del cual se va a obtener el autovalor es $\ket{\psi}=0.38268\ket{0}-0.92388\ket{1}$ , que se puede construir aplicándole a un cubit inicializado en $\ket{0}$ la puerta Pauli-X, seguida por una rotación en el eje $Y$ , usando RotY de $\pi/4$ radianes ( $45^\circ$ grados).

El autovector que se eligió coincide con el estado cuántico de la sección “Objetivo”. Su autovalor es $e^{\pi i}$ ( $180^\circ$ ).

Notar que se aplica una sola vez la puerta Hadamard controlada. Esto se debe a que la puerta controlada de Hadamard es Hermitiana, cumpliendo la propiedad:

\begin{cases} H^{2^i}=H& \text{si }i = 0\\ H^{2^i}=\mathbb{I}& \text{si }i > 0\\ \end{cases}

Por lo que solo es necesario aplicarla donde el número de ocurrencias no es par (solo el primer cubit).

Quirk
Qiskit

Estimación de fase con Hadamard

Código
Resultado

from qiskit import QuantumCircuit, transpile
from qiskit_aer import QasmSimulator
import math

QUBIT_COUNT = 4
QUBITS = range(QUBIT_COUNT)

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled.decompose(reps=6)).result()
    return result

def analyze_pe_results(results):
    counts = results.get_counts()
    print("Resultados:", counts)
    total = sum(counts.values())
    percentages = {key: f"{value / total*100:.2f}%" for key, value in counts.items()}
    ordered_percentages = dict(sorted(percentages.items(), key=lambda item: item[1], reverse=True))
    print("Porcentajes:", ordered_percentages)

def inverse_qft(qc):
    """
    Aplica la Transformada de Fourier Cuántica inversa al circuito
    """
    for i in range(QUBIT_COUNT-1):
        qc.h(QUBIT_COUNT-1-i)
        qc.barrier()
        for j in range(QUBIT_COUNT-i-1):
            qc.cp(-math.pi/(2**(j+1)), QUBIT_COUNT-2-i-j, QUBIT_COUNT-1-i)
        qc.barrier()

    qc.h(0)
    # swap
    qc.barrier()
    for i in range(QUBIT_COUNT//2):
        qc.swap(i, QUBIT_COUNT-i-1)


def controlled_hadamard(qc, control):
    """
    Aplica una puerta de Hadamard controlada al qubit objetivo.
    Como Hadamard controlada es una puerta hermitiana (su inversa es ella misma)
    Solo se necesita una puerta Hadamard y es en el primer qubit,
    el resto al ser cantidades pares (2 veces en el segundo, 4 en el tercero, etc)
    se cancelan
    """
    if control & 1:
        qc.ch(control>>1, QUBIT_COUNT)

def phase_estimation(qc,  cont_u):
    """
    Realiza la estimación de fase cuántica en un circuito
    """
    qc.h(QUBITS)
    qc.barrier()

    for j in range(QUBIT_COUNT):
        cont_u(qc, 1<<j)

    qc.barrier()
    inverse_qft(qc)


qc = QuantumCircuit(QUBIT_COUNT+1, QUBIT_COUNT)

# inicializacion de un autovector de Hadamard
qc.x(QUBIT_COUNT)
qc.ry(math.pi/4, QUBIT_COUNT)

phase_estimation(qc, controlled_hadamard)
qc.measure(QUBITS, QUBITS)

print(qc.draw())

res = run_circuit(qc)
analyze_pe_results(res)

     ┌───┐            ░       ░       ░                                ░       ░                      ░       ░            ░ ┌───┐ ░       ┌─┐
q_0: ┤ H ├────────────░───■───░───────░──────────────────────■─────────░───────░────────────■─────────░───────░──■─────────░─┤ H ├─░──X────┤M├──────
     ├───┤            ░   │   ░       ░                      │         ░       ░            │         ░ ┌───┐ ░  │P(-π/2)  ░ └───┘ ░  │    └╥┘┌─┐
q_1: ┤ H ├────────────░───┼───░───────░────────────■─────────┼─────────░───────░──■─────────┼─────────░─┤ H ├─░──■─────────░───────░──┼──X──╫─┤M├───
     ├───┤            ░   │   ░       ░            │         │         ░ ┌───┐ ░  │P(-π/2)  │P(-π/4)  ░ └───┘ ░            ░       ░  │  │  ║ └╥┘┌─┐
q_2: ┤ H ├────────────░───┼───░───────░──■─────────┼─────────┼─────────░─┤ H ├─░──■─────────■─────────░───────░────────────░───────░──┼──X──╫──╫─┤M├
     ├───┤            ░   │   ░ ┌───┐ ░  │P(-π/2)  │P(-π/4)  │P(-π/8)  ░ └───┘ ░                      ░       ░            ░       ░  │ ┌─┐ ║  ║ └╥┘
q_3: ┤ H ├────────────░───┼───░─┤ H ├─░──■─────────■─────────■─────────░───────░──────────────────────░───────░────────────░───────░──X─┤M├─╫──╫──╫─
     ├───┤┌─────────┐ ░ ┌─┴─┐ ░ └───┘ ░                                ░       ░                      ░       ░            ░       ░    └╥┘ ║  ║  ║
q_4: ┤ X ├┤ Ry(π/4) ├─░─┤ H ├─░───────░────────────────────────────────░───────░──────────────────────░───────░────────────░───────░─────╫──╫──╫──╫─
     └───┘└─────────┘ ░ └───┘ ░       ░                                ░       ░                      ░       ░            ░       ░     ║  ║  ║  ║
c: 4/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩══╩══╩═
                                                                                                                                         3  0  1  2
Resultados: {'1000': 1024}
Porcentajes: {'1000': '100.00%'}

Interpretando el resultado, se obtiene $\ket{1000}$ como medición para los primeros 4 cubits. Esto implica haber leído el número $0.1000_2$ = $0.5_{10}$ . Para obtener el autovalor, se inserta este valor en el exponencial: