Algoritmo de Shor

El algoritmo de Shor es un algoritmo cuántico desarrollado por Peter Shor en 1994, diseñado para factorizar números enteros de manera eficiente.

Su importancia radica en que puede resolver este problema en tiempo polinomial, en contraste con los mejores algoritmos clásicos conocidos, que requieren tiempo subexponencial o exponencial.

La aplicación más destacada está en la criptografía, ya que amenaza la seguridad de los sistemas basados en la factorización de números grandes, como RSA.

Objetivo

El objetivo del algoritmo de Shor es encontrar los factores de un número entero compuesto $N$.

La clave del algoritmo radica en identificar el período de la función $f(r) = x^r\ mod\ N$, donde $N$ es el número que se quiere factorizar, $x$ es un número elegido al azar tal que $1<x<N$ y $x$ es coprimo de $N$ (es decir, $x$ y $N$ no comparten factores primos), y $r$ es el período buscado.

Para lograrlo, utiliza un enfoque híbrido que combina cálculos clásicos con una subrutina cuántica basada en la estimación de fases.

Intuición

Factorizar un número $N$ implica encontrar dos números $p$ y $q$ tal que $N=pq$.

Otra forma de expresar este problema es a partir de la búsqueda del período u orden de un número $x^r$, tal que $x^r\ mod\ N=1$, y $r$ debe ser lo más chico posible y mayor a $0$. Por ejemplo:

$$x=4,\ N=5\\ x^0\ mod\ N=4^0\ mod\ 5=1\\ x^1\ mod\ N=4^1\ mod\ 5=4\\ x^2\ mod\ N=4^2\ mod\ 5=1\\ x^3\ mod\ N=4^3\ mod\ 5=4\\ x^4\ mod\ N=4^4\ mod\ 5=1\\ \vdots$$

En este caso $r=2$, por lo que cada 2 valores se repite la secuencia.

Una vez identificado $r$, se obtienen los factores de $N$ de la siguiente manera ($gcd$ significa Greatest Common Divisor, que en español se traduce como $mcd$, Máximo Común Divisor):

$$p=gcd(x^{r/2}-1,N)=gcd(4^{2/2}-1,N)=1\\ q=gcd(x^{r/2}+1,N)=gcd(4^{2/2}+1,N)=5\\$$

El algoritmo de Shor resuelve el problema de factorización utilizando una solución mixta, con componentes clásicos y con un componente cuántico que resuelve el problema de búsqueda del orden.

Este algoritmo tiene tres etapas clave:

1. Clásico: Inicialización y selección de candidato

2. Cuántico: Estimación de fases aplicado al candidato

3. Clásico: Obtención del orden y los factores de $N$

Estos pasos se pueden descomponer en componentes funcionales más chicos y menos misteriosos:

Figura (1): Diagrama del algoritmo de Shor, identificando sus componentes funcionales clásicas y cuánticas.

Los componentes funcionales de este algoritmo se pueden a reducir a los siguientes pasos:

1. Clásico: Si $N$ es par, $p=2$ y $q=N/2$. Terminar.

2. Clásico: Si $N$ es una potencia de números primos, existe un algoritmo clásico eficiente para obtener $r$ y por lo tanto los factores $p$ y $q$. Terminar.

3. Clásico: Si $N$ no es par ni una potencia de números primos, obtener un número entre $1 < x < N$, tal que $v=gcd(x,N)$. Si $v\neq 1$, entonces $p=v$ y $q=N/v$. Terminar.

4. Cuántico: Si $v=1$ (son coprimos), obtener $\widetilde{s/r}$ usando la subrutina cuántica de estimación de fases.

5. Clásico: Obtener $r$ de $\widetilde{s/r}$ utilizando el algoritmo de fracciones continuas.

6. Clásico: Si $r$ es impar volver al paso 3. Verificar que $x^r\ mod\ N=1$, y que $b=x^{r/2}\ mod\ N$ tal que $b\neq N-1$ y $b \neq 1$, en caso contrario volver al paso 3.

7. Clásico: Obtener los factores:

   $p=gcd(x^{r/2}-1,N), q=gcd(x^{r/2}+1,N)$

Resolviendo estos pasos se soluciona el problema de factorización. En las próximas secciones se profundiza matemáticamente y se implementan estos pasos.

Solución

A continuación se divide la explicación de la solución en las tres etapas definidas previamente, a modo de simplificar la lectura del artículo.

Inicialización y selección de candidato

Antes de siquiera elegir el candidato, se verifica que $N$ no sea par. En caso contrario los factores son obvios, $p=2$ y $q=N/2$.

Verificar que el número sea primo antes de empezar es ideal para evitar la búsqueda de factores no existentes (además de $1$ y de sí mismo).

Por otra parte, si $N$ es una potencia de números primos, es decir $N=c^k$ siendo $c$ un número primo, se puede obtener su exponente $k$ con un algoritmo clásico eficiente. Así, $p=c$ y $q=c^{k-1}$.

Generar un valor aleatorio de $x$ tal que $1 < x < N$. Verificar $v=gcd(x,N)$, si $v$ es diferente a $1$, significa que no son coprimos, por lo que $v$ es un factor, obteniendo $p=v$ y $q=N/v$.

Si $v=1$, se procede a la estimación de fases aplicada a $x$.

Estimación de fases aplicado al candidato

La estimación de fases permite obtener el autovalor de un autovector para una operación U. Este requiere tres parámetros como entrada:

• El primero, $q_{salida}$, es un registro inicializado en $0$ donde se obtendrá $\widetilde{\varphi}$, la fracción binaria del ángulo del autovalor $e^{2\pi i \widetilde{\varphi}}$. Su tamaño condiciona la precisión de la fracción. A mayor tamaño, mayor precisión.
• Por otra parte, el segundo parámetro es la puerta controlada de U.
• Finalmente, el tercer parámetro es $q_{entrada}$, un registro que representa el autovector de U, del cual se quiere obtener su autovalor.

El primer parámetro es fácil de preparar: un registro de cubits inicializado en $\ket{0}$. El segundo depende de U, la cual se define a continuación.

Se define U en una forma general de la siguiente manera:

$$U\ket{y}=\ket{xy\ mod\ N}$$

Aplicar U reiteradas veces sobre $\ket{1}$ retorna una potencia de $x$:

$$\begin{align} U^0\ket{1}&=\ket{x^{0}\ mod\ N}=\ket{1\ mod\ N}\\ U^1\ket{1}&=\ket{x^{1}\ mod\ N}\\ U^2\ket{1}&=\ket{x^{2}\ mod\ N}\\ \vdots&\\ U^r\ket{1}&=\ket{x^{r}\ mod\ N}=\ket{x^0\ mod\ N}\\ \end{align}$$

A continuación se presenta $u_s$, un estado cuántico del cual se quiere probar que es autovector de U con autovalor $e^{2\pi i s/r}$:

$$\begin{align} \ket{u_s}&=\frac{1}{\sqrt{r}}(e^{-2\pi i s(0)/r} \ket{x^0 mod\ N}+e^{-2\pi i s(1)/r} \ket{x^1 mod\ N}+\\ &\ldots+ e^{-2\pi i s(r-1)/r} \ket{x^{r-1} mod\ N})\\ &=\frac{1}{\sqrt{r}}\sum^{r-1}_{k=0} e^{-2\pi i sk/r}\ket{x^k mod\ N}\\ \end{align}$$

Ahora se aplica U sobre $\ket{u_s}$ para verificar su autovalor.

$$\begin{align} U\ket{u_s}&=\frac{1}{\sqrt{r}}\sum^{r-1}_{k=0} e^{-2\pi i sk/r}U\ket{x^k mod\ N}\\ &=e^{2\pi i s/r}\ket{u_s} \end{align}$$

Cálculo

Por otra parte, al saber que $\ket{u_s}$ es autovector de U, ocurre el fenómeno de retroceso de fase cuando se aplica la puerta controlada de U:

$$CU\ket{1}\ket{u_s}=e^{2\pi i s/r}\ket{1}\ket{u_s}$$

Para conseguir el tercer parámetro, se debe obtener el estado $\ket{u_s}$, el cual se sabe que es autovector de U. Se construye una superposición de $\ket{u_s}$ que suple esta necesidad:

$$\begin{align} \frac{1}{\sqrt{r}}\sum_{s=0}^{r-1}\ket{u_s}&=\ket{1} \end{align}$$

Cálculo

Así, se tienen los tres parámetros necesarios para la implementación de estimación de fase, por lo que se obtiene el siguiente circuito:

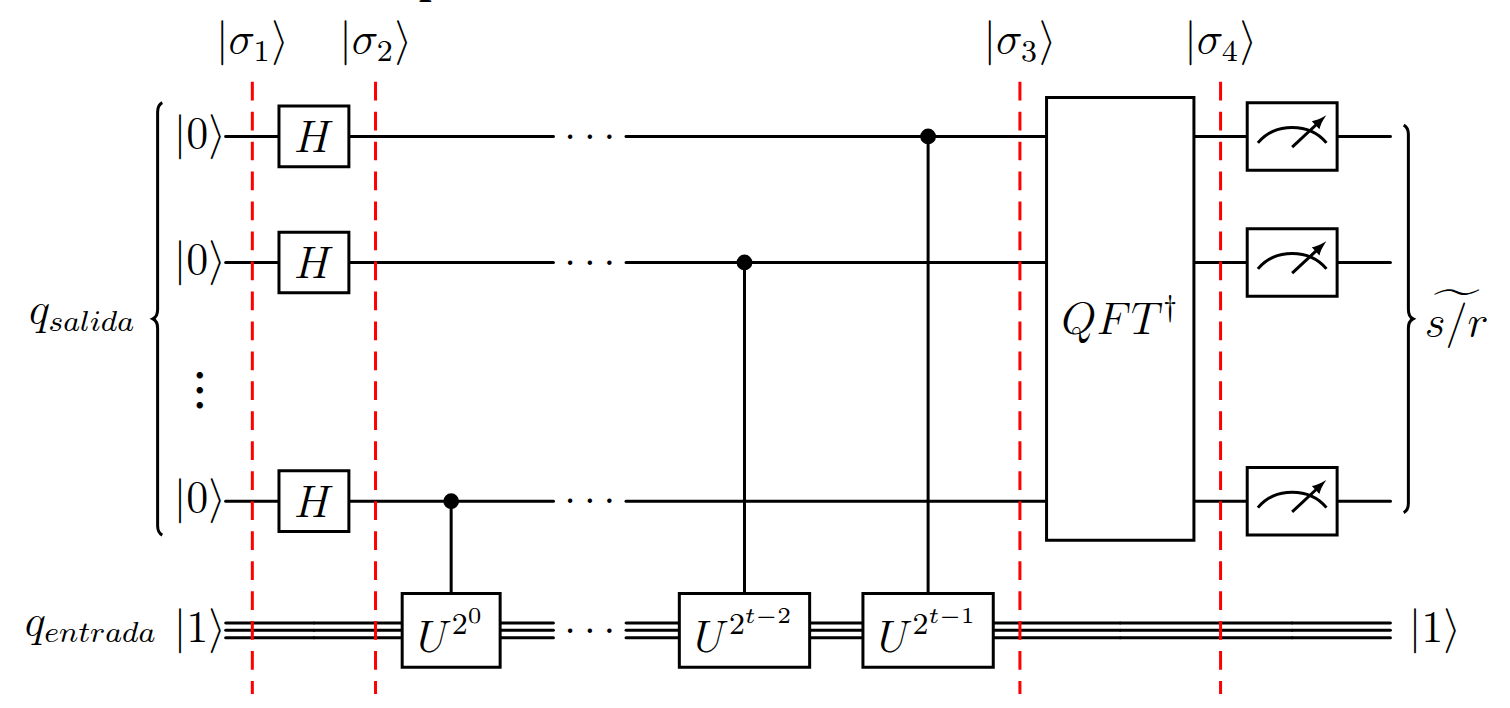
Figura (2): Estructura de la primitiva EF aplicada al algoritmo de Shor.

Se aplica el algoritmo de estimación de fases sobre $\ket{0}\ket{1}$. Como el autovalor de $\ket{1}$ es $e^{2\pi i s/r}$, el resultado es:

$$\begin{align} EF\ket{0}\ket{1}&=\ket{\widetilde{s/r}}\ket{1} \end{align}$$

Cálculo

Se obtiene finalmente el valor de $\widetilde{s/r}$ luego de aplicar una lectura en $q_{salida}$. Este valor es estimado a un nivel de precisión dependiente de la cantidad de cubits provistos.

Obtención del orden y los factores de N

Luego de obtener $\widetilde{s/r}$, que es una fracción binaria con formato $0.j_0j_1\ldots j_n$, se convierte la fracción binaria a una fracción decimal de la siguiente manera:

$$\begin{align} j=0.j_{n-1}j_{n-2}\ldots j_0&, j_i \in \{0,1\}, 0\leq i \leq n\\ l=0.l_{m-1}l_{m-2}\ldots l_0&, l_h \in \{0,1,2,3,4,5,6,7,8,9\}, 0\leq h \leq m\\ \widetilde{s/r}&=j\\ &=0.j_{n-1}j_{n-2}\ldots j_0\\ &=0+j_{n-1}2^{-1}+j_{n-2}2^{-2}+\ldots +2^{n-1}j_0\\ &=0.l_{m-1}l_{m-2}\ldots l_0\\ &=l \end{align}$$

Una vez obtenido el valor de la fracción decimal, se utiliza un algoritmo para convertir de la fracción decimal a una fracción continua que tiene el siguiente formato:

$$x=b_0+\frac{1}{b_1+\frac{1}{b_2+\frac{1}{\ddots}}}$$

El resultado de este algoritmo será un arreglo de valores enteros $c_f$ que representa la fracción continua, $c_f=[b_0,b_1,b_2,\ldots]$. Por ejemplo, con el valor $0.1562$:

$$\begin{align} 0.1562&=\frac{1562}{10000}\\ &=0+\frac{1}{\frac{10000}{1562}}\\ &=0+\frac{1}{6+\frac{628}{1562}}\\ &\quad\vdots\\ &=0+\frac{1}{6+\frac{1}{2+\frac{1}{2+\frac{1}{19+\frac{1}{8}}}}} \end{align}$$

Se obtiene la fracción continua como un arreglo de los valores enteros: $[0,6,2,2,19,8]$

A partir de este arreglo $c_f$ es posible conseguir el numerador y denominador de la fracción:

$$\begin{align} s_0 = 1,& \quad r_0 = 0\\ b_k \in c_f,& \quad 0\leq k,g < |c_f|\\ s_k &= r_{k-1} + s_{k-1} \cdot b_k\\ r_k &= s_{k-1}\\ s=s_{g}, & \quad r=r_{g},\quad r_g=max(r_k)|r_k<N \end{align}$$

Por lo que se extrae $r$ a partir de la fracción continua, siendo este el valor con mayor precisión posible de $r_k$ menor a $N$.

El último paso a realizar es comprobar que $r$ es un valor correcto y extraer los factores. En todos los casos en los que $r$ no sea correcto, se debe elegir un nuevo candidato y reiterar el algoritmo cuántico para obtener otro valor de $r$ posible.

El valor de $r$ es correcto cuando es par, es decir que $r\ mod\ 2=0$. A su vez, tiene que cumplir que $x^r\ mod\ N=1$, siendo esta la premisa del problema del orden.

Por otra parte se computa $y=x^{r/2}\ mod\ N$ y se verifica que $y\neq 1$, $y\neq N-1$ para no obtener los factores “obvios” de $N$, es decir $1$ y $N$.

Finalmente se obtienen los valores de $p$ y $q$ de la siguiente manera:

$$p=gcd(x^{r/2}-1,N)\\ q=gcd(x^{r/2}+1,N)$$

Ejemplos

Dentro de esta sección se implementará el algoritmo de Shor. Se presentará un ejemplo simple y otro ejemplo más general, expresando limitaciones y desafíos a la hora de implementar este algoritmo.

Factorizando el número 15

Como primer ejemplo se factoriza el número $15$ con el candidato $7$, cuyos factores $p$ y $q$ son $3$ y $5$.

Los ejemplos con Quirk comprenden la parte cuántica del algoritmo, por lo que luego se debe realizar el algoritmo de fracciones continuas para obtener los factores $p$ y $q$.

Por otra parte en el ejemplo de Qiskit, se resuelve el problema completo, con partes de computación clásica y cuántica.

Quirk

Se interpreta $s/r$ como una fracción binaria.

Por ejemplo si se obtiene el valor $11000000_2=2^{-1}+2^{-2}=0.75_{10}$

Luego, con fracciones continuas se tiene que $0.75=[0,1,3]$. Finalmente, $r=4$.

Como resultado, $p=gcd(7^2-1,15)=3$, $q=gcd(7^2+1,15)=5$.

Nota

Notar que de los valores posibles de $s/r$, que son: 0, 1/4, 1/2, 3/4, los únicos que cumplen con $7^r\ mod\ N = 1$ son los que tienen $r=4$. Por lo tanto, si se obtiene un $r$ diferente a $4$ se debe reiterar el procesamiento.

Qiskit

Main

import sys
import random
from math import gcd
from modules.initialization import initialization
from modules.continued_fractions import get_order
from modules.shor_phase_estimation import shor_cmod15

N=15
res = initialization(N)
finished = False
max_tries = 1000000
while not finished and max_tries > 0:
    max_tries -= 1
    candidate = random.choice([7])
    if gcd(N, candidate) != 1:
        continue
    s_over_r_results = shor_cmod15(candidate)
    s_over_r_binary = max(s_over_r_results, key=s_over_r_results.get)
    r = get_order(s_over_r_binary, N)
    if r == -1:
        continue
    print(f"Candidato: {candidate}, r: {r}, s_sobre_r: {s_over_r_binary}")
    print(f"{candidate}^{r} mod {N}: {candidate**r % N}")
    if (
        r % 2 == 1
        or candidate**r % N != 1
        or candidate ** (r // 2) % N == 1
        or candidate ** (r // 2) % N == N - 1
    ):
        print("Obtener otro candidato.")
        continue
    p = gcd(N, candidate ** int(r / 2) - 1)
    q = gcd(N, candidate ** int(r / 2) + 1)

    finished = True
    print(f"p: {p}, q: {q} [Shor]")

if not finished:
    print("Fallo al factorizar N.")
    sys.exit(1)

Inicio

from math import sqrt, ceil
import sys

def is_prime(n: int) -> bool:
    """
    Determina si un número es primo.
    """
    if n < 2:
        return False
    for i in range(2, n):
        if n % i == 0:
            return False
    return True

def eratosthenes(n):
    """
    Criba de Eratóstenes para encontrar los números primos menores o iguales a n.
    """
    multiples = []
    for i in range(2, n+1):
        if i not in multiples:
            for j in range(i*i, n+1, i):
                multiples.append(j)
    return [x for x in range(2, n+1) if x not in multiples]


def power_of_prime(primes, N):
    """
    Determina si N es una potencia de un número primo.
    """
    for p in primes:
        if N % p == 0:
            exp=0
            while N % p == 0:
                N = N // p
                exp += 1
            if N == 1:
                return p, exp
            else:
                return -1,-1
    return -1,-1


def initialization(N):
    if N % 2 == 0:
        print(f"p: 2, q: {int(N/2)} [N es par]")
        sys.exit(0)

    if is_prime(N):
        print(f"p: {N}, q: 1 [N es primo]")
        sys.exit(0)

    prime_factors = eratosthenes(ceil(sqrt(N)))
    x, exp = power_of_prime(prime_factors, N)
    if x != -1:
        print(f"p: {x}, q: {x**(exp-1)} [N es potencia de un número primo]")
        sys.exit(0)

Shor

from qiskit import QuantumCircuit, transpile
from qiskit_aer import QasmSimulator
import numpy as np

N_COUNT = 8  # qubits de salida

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled.decompose(reps=6)).result()
    return result

def c_amod15(a, power):
    """
    Puerta controlada de multiplicación por a módulo 15.
    """
    if a not in [2,4,7,8,11,13]:
        raise ValueError("'a' debe ser 2,4,7,8,11 o 13")
    U = QuantumCircuit(4)
    for _iteration in range(power):
        if a in [2,13]:
            U.swap(2,3)
            U.swap(1,2)
            U.swap(0,1)
        if a in [7,8]:
            U.swap(0,1)
            U.swap(1,2)
            U.swap(2,3)
        if a in [4, 11]:
            U.swap(1,3)
            U.swap(0,2)
        if a in [7,11,13]:
            for q in range(4):
                U.x(q)
    U = U.to_gate()
    U.name = f"{a}^{power} mod 15"
    c_U = U.control()
    return c_U

def qft_dagger(n):
    """
    Aplica la Transformada de Fourier Cuántica inversa de n qubits al circuito
    """
    qc = QuantumCircuit(n)
    # Don't forget the Swaps!
    for qubit in range(n//2):
        qc.swap(qubit, n-qubit-1)
    for j in range(n):
        for m in range(j):
            qc.cp(-np.pi/float(2**(j-m)), m, j)
        qc.h(j)
    qc.name = "QFT†"
    return qc

def shor_cmod15(a):
    """
    Estimación de fase aplicada a buscar el orden de N=15
    """
    # N_COUNT qubits de salida, y 4 qubits para U (qubits de entrada)
    qc = QuantumCircuit(N_COUNT + 4, N_COUNT)

    # creación de superposición
    for q in range(N_COUNT):
        qc.h(q)

    # inicialización de qubits de entrada en |1>
    qc.x(N_COUNT)

    # aplicación de puertas controladas
    for q in range(N_COUNT):
        qc.append(c_amod15(a, 2**q),
                 [q] + [i+N_COUNT for i in range(4)])

    # inversa QFT
    qc.append(qft_dagger(N_COUNT), range(N_COUNT))

    # medición
    qc.measure(range(N_COUNT), range(N_COUNT))
    print(qc.draw(fold=-1))

    res=run_circuit(qc)
    return res.get_counts()

Fracción

def decimal_from_binary(binary: str):
    """
    Convierte un número binario a un número decimal.
    """
    decimal = 0
    for i in range(len(binary)):
        decimal += int(binary[i]) * 2 ** -(i + 1)
    fraction_num = int(decimal * 10 ** len(binary))
    fraction_denom = int(10 ** len(binary))
    return fraction_num, fraction_denom


def continued_fraction(num: int, denom: int, res=[], debug=False):
    """
    Convierte un decimal a una fracción continua.
    """
    division = denom // num
    rest = denom % num
    res.append(division)
    if debug:
        print("[num]:", num, "[denom]:", denom, "[division]:", division, "[rest]:", rest)
    if rest == 0:
        return [0] + res
    return continued_fraction(rest, num, res, debug=debug)


def from_continued_fraction(continued_fraction):
    """
    Convierte una fracción continua a la fracción correspondiente.
    """
    num, denom = 1, 0
    for u in reversed(continued_fraction):
        num, denom = denom + num * u, num
    return num, denom


def get_order(binary_decimal: str, N: int, debug=False):
    fraction_num, fraction_denom = decimal_from_binary(binary_decimal)
    if fraction_num == 0:
        return -1
    if debug:
        print(f"Fracción: {fraction_num}/{fraction_denom}")
    fractions = continued_fraction(fraction_num, fraction_denom, res=[], debug=debug)
    if debug:
        print("Fracción continua:", fractions)

    i = 1
    finish = i-1 == len(fractions)
    order=0
    while not finish:
        s, r = from_continued_fraction(fractions[0:i])
        if debug:
            print("[s]:", s, "[r]:", r)
        if r > N:
            break
        i += 1
        finish = i-1 == len(fractions)
        order = r

    return order

Resultado

      ┌───┐                                                                                                                             ┌───────┐┌─┐
 q_0: ┤ H ├───────■─────────────────────────────────────────────────────────────────────────────────────────────────────────────────────┤0      ├┤M├─────────────────────
      ├───┤       │                                                                                                                     │       │└╥┘┌─┐
 q_1: ┤ H ├───────┼──────────────■──────────────────────────────────────────────────────────────────────────────────────────────────────┤1      ├─╫─┤M├──────────────────
      ├───┤       │              │                                                                                                      │       │ ║ └╥┘┌─┐
 q_2: ┤ H ├───────┼──────────────┼──────────────■───────────────────────────────────────────────────────────────────────────────────────┤2      ├─╫──╫─┤M├───────────────
      ├───┤       │              │              │                                                                                       │       │ ║  ║ └╥┘┌─┐
 q_3: ┤ H ├───────┼──────────────┼──────────────┼──────────────■────────────────────────────────────────────────────────────────────────┤3      ├─╫──╫──╫─┤M├────────────
      ├───┤       │              │              │              │                                                                        │  QFT† │ ║  ║  ║ └╥┘┌─┐
 q_4: ┤ H ├───────┼──────────────┼──────────────┼──────────────┼──────────────■─────────────────────────────────────────────────────────┤4      ├─╫──╫──╫──╫─┤M├─────────
      ├───┤       │              │              │              │              │                                                         │       │ ║  ║  ║  ║ └╥┘┌─┐
 q_5: ┤ H ├───────┼──────────────┼──────────────┼──────────────┼──────────────┼───────────────■─────────────────────────────────────────┤5      ├─╫──╫──╫──╫──╫─┤M├──────
      ├───┤       │              │              │              │              │               │                                         │       │ ║  ║  ║  ║  ║ └╥┘┌─┐
 q_6: ┤ H ├───────┼──────────────┼──────────────┼──────────────┼──────────────┼───────────────┼───────────────■─────────────────────────┤6      ├─╫──╫──╫──╫──╫──╫─┤M├───
      ├───┤       │              │              │              │              │               │               │                         │       │ ║  ║  ║  ║  ║  ║ └╥┘┌─┐
 q_7: ┤ H ├───────┼──────────────┼──────────────┼──────────────┼──────────────┼───────────────┼───────────────┼────────────────■────────┤7      ├─╫──╫──╫──╫──╫──╫──╫─┤M├
      ├───┤┌──────┴──────┐┌──────┴──────┐┌──────┴──────┐┌──────┴──────┐┌──────┴───────┐┌──────┴───────┐┌──────┴───────┐┌───────┴───────┐└───────┘ ║  ║  ║  ║  ║  ║  ║ └╥┘
 q_8: ┤ X ├┤0            ├┤0            ├┤0            ├┤0            ├┤0             ├┤0             ├┤0             ├┤0              ├──────────╫──╫──╫──╫──╫──╫──╫──╫─
      └───┘│             ││             ││             ││             ││              ││              ││              ││               │          ║  ║  ║  ║  ║  ║  ║  ║
 q_9: ─────┤1            ├┤1            ├┤1            ├┤1            ├┤1             ├┤1             ├┤1             ├┤1              ├──────────╫──╫──╫──╫──╫──╫──╫──╫─
           │  7^1 mod 15 ││  7^2 mod 15 ││  7^4 mod 15 ││  7^8 mod 15 ││  7^16 mod 15 ││  7^32 mod 15 ││  7^64 mod 15 ││  7^128 mod 15 │          ║  ║  ║  ║  ║  ║  ║  ║
q_10: ─────┤2            ├┤2            ├┤2            ├┤2            ├┤2             ├┤2             ├┤2             ├┤2              ├──────────╫──╫──╫──╫──╫──╫──╫──╫─
           │             ││             ││             ││             ││              ││              ││              ││               │          ║  ║  ║  ║  ║  ║  ║  ║
q_11: ─────┤3            ├┤3            ├┤3            ├┤3            ├┤3             ├┤3             ├┤3             ├┤3              ├──────────╫──╫──╫──╫──╫──╫──╫──╫─
           └─────────────┘└─────────────┘└─────────────┘└─────────────┘└──────────────┘└──────────────┘└──────────────┘└───────────────┘          ║  ║  ║  ║  ║  ║  ║  ║
 c: 8/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩══╩══╩══╩══╩══╩══╩═
                                                                                                                                                  0  1  2  3  4  5  6  7
Candidato: 7, r: 4, s_sobre_r: 11000000
7^4 mod 15: 1
p: 3, q: 5 [Shor]

Factorizando números más grandes

A la hora de factorizar números más grandes se presentan dos problemas.

El primero es el físico. Al no existir máquinas cuánticas con cubits lógicos suficientes, se emula su funcionamiento en computadoras clásicas. Este procedimiento es muy costoso, ya que el crecimiento en cantidad de operaciones es exponencial.

El segundo problema tiene que ver con la implementación de la exponencialización modular. En el ejemplo previo se utilizó una puerta que calculaba el módulo con $N=15$ y se repitió de forma exponencial la utilización de esta puerta según el cubit, es decir, una vez en el primer cubit, 2 veces en el segundo cubit, 4 veces en el tercero, etc.

La aplicación exponencial de las puertas controladas de módulo deshacen la ventaja exponencial provista por el algoritmo. Existen circuitos eficientes$^{[1][2]}$ que resuelven este problema. Debido al costo de emularlos, se decidió evitar la implementación de un algoritmo general de Shor en Qiskit.

Quirk

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 7.9 y 7.10, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Video

Quantum Computing Course: 3.8 Shor's Algorithm (Quantum Soar) [Inglés]

Libro

Capítulo 5.3 y 5.4.1, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Video

Phase Estimation and Factoring | Understanding Quantum Information & Computation - Lesson 07 (Qiskit) [Inglés]

Video

Quantum Order-Finding Subroutine of Shor's Factoring Algorithm, Phase Estimation Quantum Circuit (Elucyda) [Inglés]

Otros

Shor's Quantum Factoring Algorithm (Craig Gidney) [Inglés]

Otros

Quantum Computing (CST Part II) | Lecture 10: Application 1 of QFT / QPE: Factoring (Cambridge) [Inglés]

Libro

Capítulo 12, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Otros

Quantum Circuit of Modular Exponentiation in Qiskit (Writika Sarkar; Soham Chatterjee; Shree Ganesh SJ) [Inglés]

Otros

[1] Implementation Shor's Algorithm in Qiskit (Rui Maia; Tiago Leao) [Inglés]

Otros

[2] Shor's factoring algorithm implementation (Qiskit) [Inglés]

Otros

Fracción continua generalizada (Wikipedia) [Español]

Otros

Shor's algorithm python notebook (Qiskit) [Inglés]

Paper

Factoring with n + 2 clean qubits and n − 1 dirty qubits (Craig Gidney) [Inglés]

Paper

Circuit for Shor’s algorithm using 2n+3 qubits (Stáphane Beauregard) [Inglés]