Transformada de Fourier cuántica

La transformada de Fourier cuántica (QFT) es una solución cuántica similar a su variante clásica (transformada de Fourier discreta o DFT), que es utilizada en distintos algoritmos cuánticos.

Por ejemplo, el algoritmo de Shor y la estimación de fases utilizan esta primitiva.

Objetivo

La primitiva QFT permite obtener información acerca de las frecuencias de repetición de las fases relativas en un estado cuántico. También existe su operación inversa, que permite convertir una frecuencia en diferencias de fases relativas de un estado cuántico.

Ciertas bibliografías expresan este objetivo en transformar la base computacional a base de Fourier:

• La base computacional es la base Z.
• La base de Fourier es otra forma de expresar números pero mediante el comportamiento del eje $Z$ en un estado cuántico (fase relativa).

Nota

Se puede ver el cambio de base observando la representación de la esfera de Bloch.

Solución

La transformación de QFT es expresada en la literatura en forma de matriz de la siguiente manera (es igual a DFT pero con el ángulo opuesto):

$$F_N=\frac{1}{\sqrt{N}} \begin{bmatrix} 1&1&1&1&\ldots&1\\ 1&\omega_N&\omega_N^2&\omega_N^3&\ldots&\omega_N^{N-1}\\ 1&\omega_N^2&\omega_N^4&\omega_N^6&\ldots&\omega_N^{2(N-1)}\\ 1&\omega_N^3&\omega_N^6&\omega_N^9&\ldots&\omega_N^{3(N-1)}\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\ 1&\omega_N^{N-1}&\omega_N^{2(N-1)}&\omega_N^{2(N-1)}&\ldots&\omega_N^{(N-1)(N-1)}\\ \end{bmatrix}$$

Donde $\omega_N=e^{\frac{2\pi i}{N}}$

Es posible definir un circuito de QFT utilizando puertas Hadamard, puertas de fase controladas $R_r$, y puertas Swap.

La puerta $R_r$ es una abreviación de RotZ y se define de la siguiente manera:

$$R_r=RotZ(e^{2\pi i/2^r})=\begin{bmatrix} 1&0\\ 0&e^{2\pi i/2^r}\\ \end{bmatrix}= \begin{bmatrix} 1&0\\ 0&\omega_{2^r}\\ \end{bmatrix}$$

Con esto en consideración, el algoritmo $QFT_n$ sigue una estructura fácilmente generalizable, donde $n$ es la cantidad de cubits presentes.

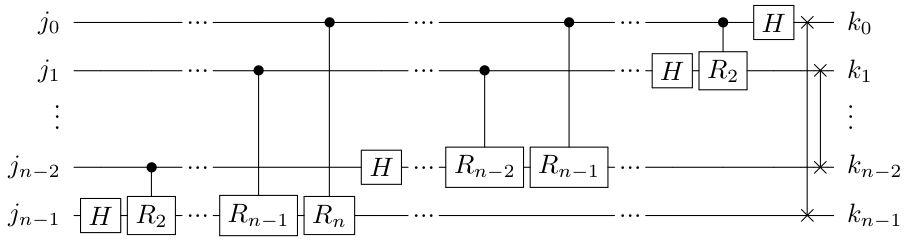
Figura (1): Estructura de la primitiva QFT de forma general (Wong).

En este caso se utiliza $j_{n-1}, j_{n-2}, \ldots, j_0$ para representar los cubits de entrada que conforman el estado cuántico $j$:

$$j=j_{n-1}j_{n-2}\ldots j_0$$

Por otra parte, se utiliza $0.j_mj_{m-1}\ldots j_l$ para denotar fracciones usando binarios, cuyo valor en decimal es el siguiente:

$$0.j_mj_{m-1}\ldots j_{l}=j_m/2+j_{m-1}/4+\ldots+j_l/2^{m-l+1}$$

Finalmente definimos QFT en notación bra-ket como:

$$\begin{align} QFT\ket{j}=&\frac{1}{2^{n/2}}\sum_{k=0}^{2^n-1}e^{2\pi i j k /2^n}\ket{k}\\ =&\frac{1}{2^{n/2}}(\ket{0}+e^{2\pi i 0.j_0}\ket{1})(\ket{0}+e^{2\pi i 0.j_1j_0}\ket{1})\\ &\ldots(\ket{0}+e^{2\pi i 0.j_{n-1}j_{n-2}\ldots j_0}\ket{1})\notag \end{align}$$

Se encuentran $n$ puertas Hadamard y $(n)(n+1)/2$ puertas de rotación, por lo que el orden del algoritmo es $O(n^2)=O((log_2 N)^2)$, ya que $N=2^n$.

Por otra parte, como el algoritmo de QFT es conformado por puertas unitarias. Para implementar la inversa de QFT (invQFT) basta con aplicar las operaciones conjugadas transpuestas en el orden inverso.

Quirk

QFT

Es recomendable observar este ejemplo en el propio simulador de Quirk por su tamaño.

invQFT

Es recomendable observar este ejemplo en el propio simulador de Quirk por su tamaño.

Qiskit

Código

from qiskit import QuantumCircuit, transpile
from qiskit_aer import QasmSimulator
import math

QUBIT_COUNT = 3
QUBITS = range(QUBIT_COUNT)

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled).result()
    return result

def analyze_qft_results(results):
    counts = results.get_counts()
    print("Resultados:", counts)
    total = sum(counts.values())
    percentages = {key: f"{value / total*100:.2f}%" for key, value in counts.items()}
    ordered_percentages = dict(sorted(percentages.items(), key=lambda item: item[1], reverse=True))
    print("Porcentajes:", ordered_percentages)


def qft(qc):
    """
    Aplica la Transformada de Fourier Cuántica al circuito
    """
    # swap
    qc.barrier()
    for i in range(QUBIT_COUNT//2):
        qc.swap(i, QUBIT_COUNT-i-1)
    qc.barrier()

    for i in range(QUBIT_COUNT-1):
        qc.h(i)
        qc.barrier()
        for j in range(i+1):
            qc.cp(math.pi/(2**(j+1)), i-j, i+1)

    qc.h(QUBIT_COUNT-1)

def inverse_qft(qc):
    """
    Aplica la Transformada de Fourier Cuántica inversa al circuito
    """
    for i in range(QUBIT_COUNT-1):
        qc.h(QUBIT_COUNT-1-i)
        qc.barrier()
        for j in range(QUBIT_COUNT-i-1):
            qc.cp(-math.pi/(2**(j+1)), QUBIT_COUNT-2-i-j, QUBIT_COUNT-1-i)
        qc.barrier()

    qc.h(0)
    # swap
    qc.barrier()
    for i in range(QUBIT_COUNT//2):
        qc.swap(i, QUBIT_COUNT-i-1)

qc = QuantumCircuit(QUBIT_COUNT, QUBIT_COUNT)

qc.x(2) # frecuencia de la onda
qc.barrier()
inverse_qft(qc) # generar la onda
qc.barrier()
qft(qc) # obtener la frecuencia
qc.barrier()

qc.measure(QUBITS, QUBITS)
print(qc.draw())

res = run_circuit(qc)
analyze_qft_results(res)

Resultado

           ░       ░                      ░       ░            ░ ┌───┐ ░     ░  ░     ░ ┌───┐ ░                ░                         ░ ┌─┐
q_0: ──────░───────░────────────■─────────░───────░──■─────────░─┤ H ├─░──X──░──░──X──░─┤ H ├─░──■─────────────░───────────■─────────────░─┤M├──────
           ░       ░            │         ░ ┌───┐ ░  │P(-π/2)  ░ └───┘ ░  │  ░  ░  │  ░ └───┘ ░  │P(π/2) ┌───┐ ░           │             ░ └╥┘┌─┐
q_1: ──────░───────░──■─────────┼─────────░─┤ H ├─░──■─────────░───────░──┼──░──░──┼──░───────░──■───────┤ H ├─░──■────────┼─────────────░──╫─┤M├───
     ┌───┐ ░ ┌───┐ ░  │P(-π/2)  │P(-π/4)  ░ └───┘ ░            ░       ░  │  ░  ░  │  ░       ░          └───┘ ░  │P(π/2)  │P(π/4) ┌───┐ ░  ║ └╥┘┌─┐
q_2: ┤ X ├─░─┤ H ├─░──■─────────■─────────░───────░────────────░───────░──X──░──░──X──░───────░────────────────░──■────────■───────┤ H ├─░──╫──╫─┤M├
     └───┘ ░ └───┘ ░                      ░       ░            ░       ░     ░  ░     ░       ░                ░                   └───┘ ░  ║  ║ └╥┘
c: 3/═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩══╩═
                                                                                                                                            0  1  2
Resultados: {'100': 1024}
Porcentajes: {'100': '100.00%'}

Observando el circuito uno puede detectar que tanto QFT como su inversa son similares. Como curiosidad, se puede probar que aplicar tres veces QFT es equivalente a utilizar su inversa:

$$\begin{gather} F_N F_N\ket{k} =\ket{-k}=\ket{N-k}\\ F_N F_N F_N F_N \ket{k} =\ket{k} \rightarrow F_N^\dag = F_N F_N F_N \\ F_N^\dag F_N^\dag F_N^\dag F_N^\dag \ket{k} =\ket{k} \rightarrow F_N = F_N^\dag F_N^\dag F_N^\dag \end{gather}$$

Ejemplos

En esta sección se elaboran distintos ejemplos que permitan demostrar el funcionamiento de QFT para casos específicos.

Usando QFT

Se presentan tres ejemplos. En estos ejemplos se obtiene la frecuencia del patrón de fases a partir de un estado cuántico dado.

En el primer ejemplo el patrón se repite 8 veces, en el segundo 4 veces y en el tercero se repite 2 veces, pero en formato de señales cuadradas.

Círculos

Ejemplo 1

Estado inicial del algoritmo, se repite ocho veces el patrón de fases.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

QFT

Luego de aplicar QFT se revela que la frecuencia del estado cuántico es 8.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Ejemplo 2

Estado inicial del algoritmo. Se repite cuatro veces el patrón de fases.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

QFT

Luego de aplicar QFT se revela que la frecuencia del estado cuántico es 4.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Ejemplo 3

Estado inicial del algoritmo, se repite dos veces el patrón de fases, pero representan señales “cuadradas”.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

QFT

Luego de aplicar QFT se revela que la frecuencia del estado cuántico es probable que sea 2, pero existen otros valores posibles.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Nota

En estos casos, como utilizamos señales reales y no complejas, es útil descartar aquellos valores mayores a la mitad de los valores posibles. Es decir, se toman los primeros 16/2+1=9 valores, ya que el resto solo representa un espejo de la frecuencia de la señal.

Quirk

Ejemplo 1

Ejemplo 2

Ejemplo 3

Nota

En estos casos, como utilizamos señales reales y no complejas, es útil descartar aquellos valores mayores a la mitad de los valores posibles. Es decir, se toman los primeros 16/2+1=9 valores, ya que el resto solo representa un espejo de la frecuencia de la señal.

Usando invQFT

En el formato contrario a la sección anterior, se presentarán ejemplos de frecuencias y se convertirán a patrónes de fases relativas utilizando invQFT.

En el primer ejemplo se obtendrá la señal con frecuencia 2, y en el segundo ejemplo la señal con frecuencia 1.

Círculos

Ejemplo 1

Estado inicial del algoritmo, se marca como frecuencia el número “2”.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

invQFT

Luego de aplicar la inversa de QFT, se genera la señal con frecuencia 2.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Ejemplo 2

Estado inicial del algoritmo, se marca como frecuencia el numero “1”.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

invQFT

Luego de aplicar la inversa de QFT se genera la señal con frecuencia 1.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Quirk

Ejemplo 1

Ejemplo 2

Consideraciones

La implementación de QFT varía según la bibliografía. Puede presentarse con diferentes puertas, o en diferente orden, o con/sin puertas de intercambio.

A su vez, existen casos donde se interpreta QFT con la misma definición que DFT y en otros casos como su inversa (ángulos opuestos).

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 7, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Libro

Capítulo 7.7.3, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Video

Quantum Computing Course: 3.6 Quantum Fourier Transform (Quantum Soar) [Inglés]

Video

Phase Estimation and Factoring | Understanding Quantum Information & Computation - Lesson 07 (Qiskit) [Inglés]

Video

Inverse n-qubit Quantum Fourier Transform and Phase Estimation Quantum Circuit (Elucyda) [Inglés]

Video

Quantum Fourier Transform, Tensor Product Representation, Analogy with Discrete Fourier Transform (Elucyda) [Inglés]

Libro

Capítulo 5.1, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Otros

Quantum Computing (CST Part II) | Lecture 9: Quantum Fourier Transform & Quantum Phase Estimation (Cambridge) [Inglés]

Otros

Transformada cuántica de Fourier (Wikipedia) [Español]