Teleportación cuántica

Es un protocolo de comunicación donde un transmisor (Alice) envía un cubit a un receptor (Bob), utilizando un estado cuántico entrelazado compartido junto a dos bits clásicos para realizar la comunicación.

Se asume que tanto el transmisor como el receptor comparten un cubit entrelazado, es decir que: el transmisor tiene un cubit A, el receptor tiene un cubit B, y el par (A,B) está en el estado $\ket{\Phi^+}$, que es un estado de Bell.

Ademas el transmisor posee un cubit Q que es el que desea enviar al receptor, el estado de este cubit es desconocido tanto por el transmisor como el receptor. Esta transmisión implica una destrucción de información del cubit Q y del cubit A, ya que en ambos casos se miden sus estados, para luego reconstruirlo en el cubit B utilizando la información dada por las lecturas de Q y A.

Nota

La teleportación es de información cuántica y no de materia (como en las películas). A su vez, no es más rápida que la velocidad de la luz ya que se utilizan dos bits clásicos (estos se transmiten en menor velocidad que la luz) para reconstruir el cubit Q.

Protocolo

Se presenta una implementación general del protocolo de teleportación cuántica, este contiene puertas Hadamard, CNOT, Pauli-Z y una puerta genérica “U” que pretende encapsular el estado del cubit Q a transmitir. La puerta U$^{\dag}$ es la conjugada transpuesta de U, tal que UU$^{\dag}=I$.

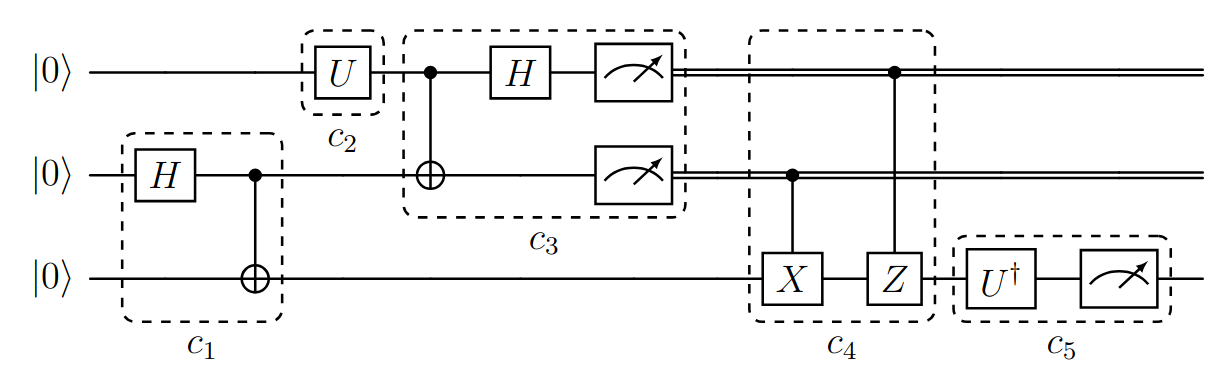
Figura (1): Protocolo de teleportación cuántico, indicando los componentes funcionales del circuito.

Dentro de los componentes, se enumeran $5$ pasos o etapas del protocolo, enumerados en un orden que pretende simular la comunicación entre dos agentes.

El primer componente $c_1$ es la creación de un par entrelazado. Se conforma el estado $\ket{\Phi^+}$, que es uno de los estados de Bell.

Luego el segundo componente $c_2$ es la preparación del mensaje. En esta etapa, utilizando la puerta genérica U, se pretende encapsular puertas e interacciones con otros cubits.

Le sigue el tercer componente $c_3$ que es el envío del mensaje, que consta de 3 pasos:

• Se entrelaza el cubit que se desea transmitir con la mitad del par entrelazado del transmisor (primera línea con segunda) utilizando la puerta $CNOT$. Esto causa que el cubit a transmitir se entrelace de forma indirecta con el cubit del receptor (primera línea con tercera).
• Aplicar una Hadamard para no perder información de magnitud y fase al medir.
• Finalmente, se realizan la medición.

El cuarto componente $c_4$ finaliza la teleportación, recibiendo el mensaje. El recibir el mensaje implica realizar cambios al cubit recibido según la medición, dando cuatro combinaciones posibles:

• En caso de que se lea un $0$ en la primera línea y un $0$ en la segunda, no es necesario realizar ningún cambio al cubit recibido.
• Si se lee un $0$ en la primera línea y un $1$ en la segunda, para que quede igual que el estado original es necesario invertir las amplitudes (aplicar $CNOT$).
• Por otro lado si lee un $1$ en la primera línea y un $0$ en la segunda, para que quede igual que el estado original es necesario aumentar la fase en $180^\circ$ (aplicar $CZ$).
• Por último si se lee un $1$ en la primera línea y un $1$ en la segunda, es necesario invertir las amplitudes y aumentar la fase en $180^\circ$ (aplicar $CNOT$ y $CZ$).

El último componente $c_5$ verifica el éxito de la teleportación. Esto se hace aplicando las puertas inversas a las recibidas en $c_2$ y midiendo el resultado. Si luego de medir resulta en $0$ significa que la teleportación fue exitosa. En caso contrario, esta falló.

Tanto los componentes $c_1$, $c_2$ y $c_5$ pueden considerarse externos al protocolo. Los componentes $c_1$ y $c_2$ pueden considerarse precondiciones para que el protocolo funcione correctamente y $c_5$ como procesamiento opcional. Ciertas bibliografías los evitan y dan por hecho.

Ejemplos

Se desarrollará un ejemplo donde se elaborará la aplicación del protocolo paso a paso.

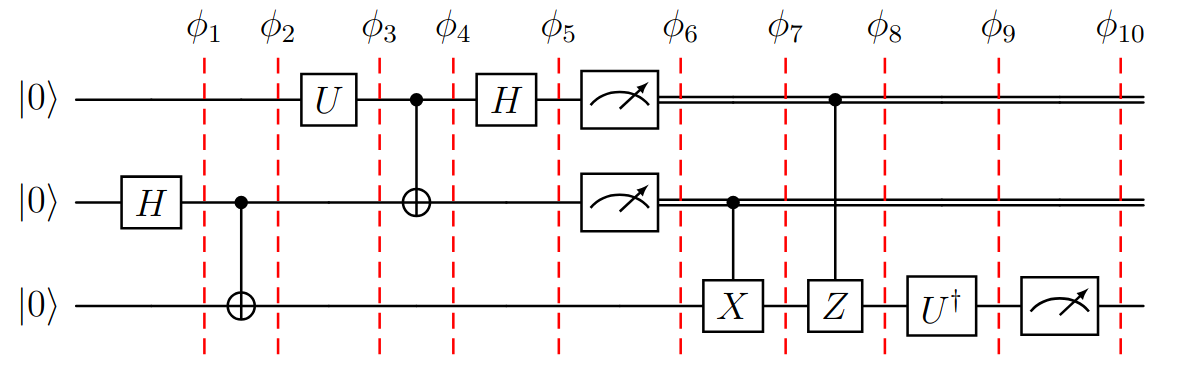
Figura (2): Protocolo de teleportación cuántico, con separadores ante la aplicación de cada puerta.

Se reemplazará la puerta genérica U con un ejemplo de puerta que represente un estado cuántico a transmitir. La misma puede observarse en la siguiente imagen:

Figura (3): Reemplazo de la puerta $U$ por una puerta con una Hadamard seguida de una puerta $T$ y finalizando con otra puerta Hadamard.

La puerta aplicada sobre un cubit inicializado en $\ket{0}$ se puede representar de la siguiente manera:

$$\ket{0}$$

$$\ket{1}$$

$\overset{H}{\rightarrow}$

$$\ket{0}$$

$$\ket{1}$$

$$\ket{0}$$

$$\ket{1}$$

$\overset{T}{\rightarrow}$

$$\ket{0}$$

$$\ket{1}$$

$$\ket{0}$$

$$\ket{1}$$

$\overset{H}{\rightarrow}$

$$\ket{0}$$

$$\ket{1}$$

Círculos

Analizaremos paso a paso el estado de los cubits según los separadores provistos en el circuito, donde \(\phi_i\) es el estado en el paso \(i\), empezando con \(i=1\) y finalizando con \(i=10\).

\(\phi_0\)

El paso $0$ representa los valores con los cuales se inicializó el circuito:

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_1\)

Luego de aplicar una Hadamard al segundo cubit, se obtiene una superposición entre $\ket{000}$ y $\ket{010}$.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_2\)

Con el paso $\phi_2$ se finaliza la componente $c_1$ creando un par entrelazado ($\Phi^+=\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})$) entre el segundo y tercer cubit.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_3\)

En el paso $\phi_3$ se aplica la puerta U, definida previamente en la figura 3, cumple la funcionalidad descrita en el componente $c_2$.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_4\)

En este paso se prepara el envío del mensaje (componente $c_3$), aplicando $CNOT$, teniendo como control el primer cubit y como objetivo el segundo cubit. El resultado de esto es el entrelazamiento del primer cubit con el segundo cubit y se crea, de forma indirecta, un entrelazamiento entre el primer cubit y el tercero (ya que estos dos estaban previamente entrelazados).

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_5\)

Seguido al anterior, se aplica una puerta Hadamard al primer cubit, dejándolo superpuesto para no perder información de magnitud y fase en el siguiente paso.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_6\)

Este paso es crucial ya que realiza el envío (finaliza el componente $c_3$) y define cómo interpretar el mensaje al receptor. Las mediciones causan una pérdida de los primeros dos cubits. Esto es necesario ya que no se pueden copiar los estados cuánticos.

Supóngase que el primer cubit, al leerlo, colapsa en un $1$ (convirtiéndose en un bit clásico), y que el segundo cubit al leerlo también colapsa en $1$, obteniendo el siguiente estado cuántico.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

Nota

Es interesante denotar que las lecturas posibles $(00, 01, 10, 11)$ corresponden con las columnas de la notación de círculos. Por ejemplo, si se hubiese leído un $1$ en el primer cubit y un $0$ en el segundo se hubiese obtenido la tercer columna (finalizando con $10$).

\(\phi_7\)

Tanto $\phi_7$ como $\phi_8$ cumplen el rol de interpretar el mensaje recibido y realizarle las transformaciones necesarias para obtener el estado original. Cumplen la función del componente $c_4$.

Dadas las lecturas definidas previamente, como el segundo cubit colapsó en $1$ se aplica una Pauli-X al tercer cubit ($CNOT$), intercambiando las magnitudes.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_8\)

De la misma manera que el paso anterior, como el primer cubit colapsó en $1$ se aplica una puerta Pauli-Z al tercer cubit ($CZ$), rotando su fase relativa en $180^{\circ}$, finalizando el componente $c_4$.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

\(\phi_9\)

Finalmente este paso cumple la función de verificar el resultado (componente $c_5$), esto conlleva aplicar la puerta inversa a U. En este caso implica aplicar la puerta Hadamard, seguida por T$^{-1}$ y finalizada por otra puerta Hadamard. Esto quiere decir que se realizan los pasos inversos que realiza U.

Al aplicarlo obtenemos que el estado es $\ket{000}$, el estado inicial, por lo que verificamos que la teleportación fue exitosa.

$$\ket{000}$$

$$\ket{001}$$

$$\ket{010}$$

$$\ket{011}$$

$$\ket{100}$$

$$\ket{101}$$

$$\ket{110}$$

$$\ket{111}$$

Quirk

Ejemplo HTH

Estado randomizado

Qiskit

Código

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister
import math

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled).result()
    return result

# estados cuánticos
sender = QuantumRegister(1, name="transmisor")
entangledpair = QuantumRegister(1, name="parentrelazado")
receiver = QuantumRegister(1, name="receptor")

# estados clásicos
sender_c = ClassicalRegister(1, name="transmisorclasico")
entangledpair_c = ClassicalRegister(1, name="parentrelazadoclasico")
receiver_c = ClassicalRegister(1, name="receptorclasico")

# circuito cuántico
qc = QuantumCircuit(
    sender, entangledpair, receiver, sender_c, entangledpair_c, receiver_c
)

# componente c1
qc.h(entangledpair)
qc.cx(entangledpair, receiver)
qc.barrier()

# componente c2, U=H T H
qc.reset(sender)
qc.h(sender)
qc.rz(math.radians(45), sender)
qc.h(sender)
qc.barrier()

# componente c3
qc.cx(sender, entangledpair)
qc.h(sender)
qc.measure(sender, sender_c)
qc.measure(entangledpair, entangledpair_c)
qc.barrier()

# componente c4
with qc.if_test((entangledpair_c, 1)):
    qc.x(receiver)
with qc.if_test((sender_c, 1)):
    qc.z(receiver)

# componente c5, U^-1 = H T^-1 H
qc.h(receiver)
qc.rz(math.radians(-45), receiver)
qc.h(receiver)
qc.measure(receiver, receiver_c)

res = run_circuit(qc)

print(qc.draw())
counts = res.get_counts()
# obtener los resultados del 3er qubit
third_qubit_sum0 = 0
third_qubit_sum1 = 0
for key in counts:
    if key[0] == "0":
        third_qubit_sum0 += counts[key]
    else:
        third_qubit_sum1 += counts[key]
print("Probabilidad de medir 0 en el receptor: ", third_qubit_sum0 / (third_qubit_sum0 + third_qubit_sum1))

Resultado

                                    ░      ┌───┐┌─────────┐┌───┐ ░      ┌───┐┌─┐ ░
             transmisor: ───────────░──|0>─┤ H ├┤ Rz(π/4) ├┤ H ├─░───■──┤ H ├┤M├─░────────────────────────────────────────────────────────────────────────
                         ┌───┐      ░      └───┘└─────────┘└───┘ ░ ┌─┴─┐└┬─┬┘└╥┘ ░
         parentrelazado: ┤ H ├──■───░────────────────────────────░─┤ X ├─┤M├──╫──░────────────────────────────────────────────────────────────────────────
                         └───┘┌─┴─┐ ░                            ░ └───┘ └╥┘  ║  ░ ┌────── ┌───┐ ───────┐ ┌────── ┌───┐ ───────┐ ┌───┐┌──────────┐┌───┐┌─┐
               receptor: ─────┤ X ├─░────────────────────────────░────────╫───╫──░─┤ If-0  ┤ X ├  End-0 ├─┤ If-0  ┤ Z ├  End-0 ├─┤ H ├┤ Rz(-π/4) ├┤ H ├┤M├
                              └───┘ ░                            ░        ║   ║  ░ └──╥─── └───┘ ───────┘ └──╥─── └───┘ ───────┘ └───┘└──────────┘└───┘└╥┘
                                                                          ║   ║       ║                   ┌──╨──┐                                       ║
    transmisorclasico: 1/═════════════════════════════════════════════════╬═══╩═══════╬═══════════════════╡ 0x1 ╞═══════════════════════════════════════╬═
                                                                          ║   0    ┌──╨──┐                └─────┘                                       ║
parentrelazadoclasico: 1/═════════════════════════════════════════════════╩════════╡ 0x1 ╞══════════════════════════════════════════════════════════════╬═
                                                                          0        └─────┘                                                              ║
      receptorclasico: 1/═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩═
                                                                                                                                                        0
Probabilidad de medir 0 en el receptor:  1.0

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 4, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Libro

Capítulo 6.5, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Video

Entanglement in Action | Understanding Quantum Information & Computation - Lesson 04 (Qiskit) [Inglés]

Libro

Capítulo 1.3.7, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Otros

Quantum Computing (CST Part II) | Lecture 6: Some Applications of Quantum Information (Cambridge) [Inglés]

Otros

Alice y Bob (Wikipedia) [Español]