Codificación superdensa

La codificación superdensa es una aplicación simple de la mecánica cuántica elemental, ya que combina todas las ideas básicas de dicha rama, y es por lo tanto un ejemplo ideal de las tareas de procesamiento de la información que pueden llevarse a cabo mediante la mecánica cuántica. Se trata de un protocolo que adquiere un rol complementario a la Teleportación cuántica. La diferencia radica en que en lugar de permitir la transmisión de un cubit usando dos bits clásicos de comunicación (con el costo de un e-bit de entrelazamiento), permite la transmisión de dos bits cásicos usando un cubit de comunicación cuántica (también con el costo de un e-bit de entrelazamiento).

Protocolo

La codificación superdensa involucra dos partes, conocidas tradicionalmente como ‘Alice’ y ‘Bob’, quienes se encuentran a una gran distancia uno de otro. Su objetivo es transmitir información clásica desde Alice hacia Bob. Supóngase que Alice posee dos bits clásicos de información que desea enviar a Bob, pero solamente tiene permitido enviarle un solo cubit. Clásicamente, Alice debería enviarle los dos bits a Bob, uno no sería suficiente porque solamente tiene dos estados $0$ o $1$ . Cuánticamente, dicha tarea puede resolverse utilizando un solo cubit mediante la codificación superdensa. Para esto, Alice y Bob deben compartir inicialmente un par de cubits en el siguiente estado de entrelazamiento:

\ket{\Phi^+} = \frac{\ket{00} + \ket{11}}{\sqrt{2}}

Donde Alice posee el primer cubit y Bob posee el segundo cubit. Notar que $\ket{\Phi^+}$ es un estado fijo, por lo cual no hay necesidad de que Alice haya enviado a Bob ningún cubit para preparar dicho estado. En su lugar, un tercero podría haber preparado el estado de entrelazamiento previamente, enviando uno de los cubits a Alice y el otro a Bob.

Dependiendo de cuál de las cuatro opciones Alice desee comunicar a Bob (00, 01, 10 o 11), ella puede aplicar puertas cuánticas a su cubit, para luego enviárselo a Bob de manera que él tenga ambos cubits.

Si Alice quiere enviar $00$ , entonces no le hace nada a su cubit, y se lo envía a Bob.
Si Alice quiere enviar $01$ , entonces aplica la puerta $X$ sobre su cubit, lo cual transforma $\ket{\Phi^+}$ en

\ket{\Psi^+} = \frac{1}{\sqrt{2}}(\ket{10} + \ket{01})

y luego envía el cubit a Bob.

Si Alice quiere enviar $10$ , entonces aplica la puerta $Z$ a su cubit, lo cual transforma $\ket{\Phi^+}$ en

\ket{\Phi^-} = \frac{1}{\sqrt{2}}(\ket{00} - \ket{11})

y luego envía su cubit a Bob.

Finalmente, si Alice quiere enviar $11$ , aplica tanto $X$ como $Z$ a su cubit. Aplicar $X$ transforma $\ket{\Phi^+}$ en $\ket{\Psi^+}$ , y aplicar $Z$ transforma $\ket{\Psi^+}$ en

\ket{\Psi^-} = \frac{1}{\sqrt{2}}(\ket{01} - \ket{10})

y luego Alice envía su cubit a Bob.

Ahora Bob posee ambos cubits, los cuales pueden estar en uno de los siguientes cuatro estados:

\ket{\Phi^+} = \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})\\ \ket{\Psi^+} = \frac{1}{\sqrt{2}}(\ket{01} + \ket{10})\\ \ket{\Phi^-} = \frac{1}{\sqrt{2}}(\ket{00} - \ket{11})\\ \ket{\Psi^-} = \frac{1}{\sqrt{2}}(\ket{01} - \ket{10})

Dado que estos estados son ortonormales, forman una base de medición llamada base de Bell. Bob puede medir los dos cubits en la base de Bell para distinguirlos, y por lo tanto determinar qué envió Alice. Este proceso se conoce como medición de Bell.

Otra forma de entender la medición de Bell consiste en aplicar $CNOT$ y luego $H \otimes I$ , para finalmente medir en la base Z. Esto es,

\begin{align} \ket{\Phi^+}&\overset{CNOT}{\longrightarrow}\frac{1}{\sqrt{2}}(\ket{00} + \ket{10})=\ket{+}\ket{0}&\overset{H\otimes I}{\longrightarrow}=\ket{00},\\ \ket{\Psi^+}&\overset{CNOT}{\longrightarrow}\frac{1}{\sqrt{2}}(\ket{01} + \ket{11})=\ket{+}\ket{1}&\overset{H\otimes I}{\longrightarrow}=\ket{01},\\ \ket{\Phi^-}&\overset{CNOT}{\longrightarrow}\frac{1}{\sqrt{2}}(\ket{00} - \ket{10})=\ket{-}\ket{0}&\overset{H\otimes I}{\longrightarrow}=\ket{10},\\ \ket{\Psi^-}&\overset{CNOT}{\longrightarrow}\frac{1}{\sqrt{2}}(\ket{01} - \ket{11})=\ket{-}\ket{1}&\overset{H\otimes I}{\longrightarrow}=\ket{11}. \end{align}

Computacionalmente este protocolo aún requiere dos cubits para funcionar, pero como protocolo de comunicación requiere que se envíe un único cubit. Generalizando la codificación superdensa, notar que si Alice y Bob comparten $n$ pares de cubits entrelazados ( $n$ e-bits conforman un total de $2n$ cubits), entonces Alice puede medir cada uno de sus $n$ cubits y enviárselos a Bob, disminuyendo notablemente la cantidad de cubits a enviar.

Por último es importante destacar que un teorema famoso en la teoría de la información cuántica, conocido como teorema de Holevo, dice que sin el uso de estados entrelazados compartidos es imposible comunicar más de un bit de información clásica enviando un solo cubit. Así, mediante la codificación superdensa, el entrelazamiento compartido permite duplicar efectivamente la capacidad de transferencia de información clásica al enviar cubits.

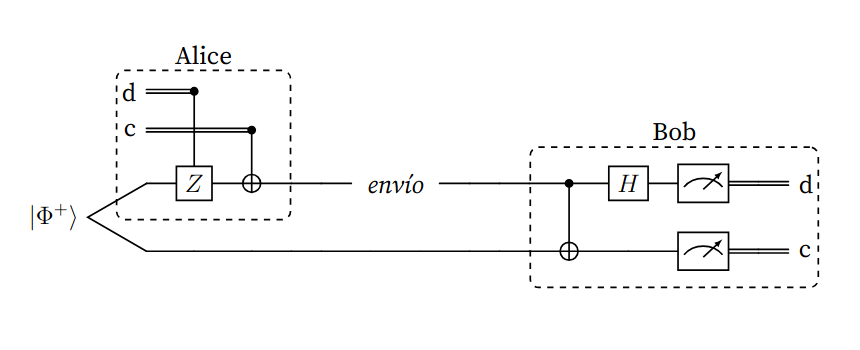
Protocolo de codificación superdensa, ubicando los cubits que poseen Alice y Bob.

Figura (1): Protocolo de codificación superdensa, indicando las responsabilidades de Alice y Bob en las distintas partes del circuito.

Ejemplos

Para finalizar este artículo se presentará un ejemplo que involucre la acción de dos cubits, donde Alice desea enviar los bits de información $11$ mediante el cubit que ella tiene en su poder. Tal como se explicó anteriormente, se asume que los dos cubits se encuentran en un estado de entrelazamiento, y que un tercero le otorgó uno a Alice y otro a Bob.

A continuación se elaborará un paso a paso de la aplicación del protocolo.

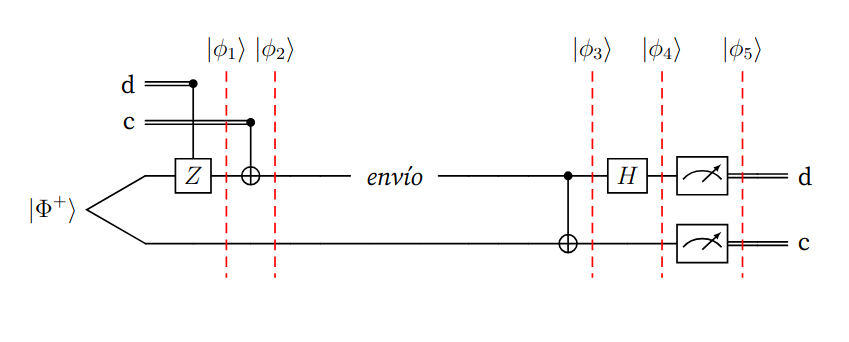
Figura (2): Protocolo de codificación superdensa, con separadores ante la aplicación de cada puerta.

Se analizará paso a paso el estado de los cubits segun los separadores provistos en el circuito, donde $\phi_i$ es el estado en el paso $i$, empezando con $i=1$ y finalizando con $i=5$.

$\phi_0$

El paso $0$ representa los valores con los cuales se inicializó el circuito. En este caso, se inicia el circuito con el estado $\ket{\Phi^+} = \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})$ , es decir, los cubits ya se encuentran entrelazados.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\phi_1$

Se aplica una puerta $CZ$ sobre el primer cubit con el valor del bit más significativo $d$ como bit de control, cuyo valor es 1, por lo que se aplica un cambio de fase en 180º sobre dicho cubit. Se alcanza el estado $\ket{\Phi^-} = \frac{1}{\sqrt{2}}(\ket{00} - \ket{11})$ .

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\phi_2$

Se aplica una puerta $CNOT$ sobre el primer cubit con el valor del bit menos significativo $c$ como bit de control, cuyo valor es 1, por lo que se aplica NOT sobre dicho cubit. Se alcanza el estado $\frac{1}{\sqrt{2}}(-\ket{01} + \ket{10})$ , que convenientemente es equivalente a $-\frac{1}{\sqrt{2}}(\ket{01} - \ket{10})$ , aplicando una fase global $-1$ .

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\phi_3$

Se opera con la puerta $CNOT$ con el primer cubit como control y el segundo cubit como target. Se alcanza el estado $-\frac{1}{\sqrt{2}}(\ket{01} - \ket{11})$ .

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\phi_4$

Se aplica Hadamard sobre el primer cubit para deshacer el entrelazamiento y poder medir los cubits. Se llega al estado $-\ket{11}$ .

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\phi_5$

Se realiza la medición sobre ambos cubits, obteniendo el valor $\ket{11}$ con $100\%$ de probabilidad (la fase global no afecta en la medición), donde el primer cubit toma el valor del bit $d$ y el segundo cubit toma el valor del bit $c$ .

Código
Resultado

from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit_aer import QasmSimulator

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled).result()
    return result

# estados cuánticos
data = QuantumRegister(2, name="data")
entangledpair = QuantumRegister(2, name="parentrelazado")

# estados clásicos
data_c = ClassicalRegister(2, name="dataclasica")
entangledpair_c = ClassicalRegister(2, name="parentrelazadoclasico")

# circuito cuántico
qc = QuantumCircuit(
    data, entangledpair, data_c, entangledpair_c
)

# Entrelazamiento de qubits
qc.h(entangledpair[0])
qc.cx(entangledpair[0], entangledpair[1])
qc.barrier()

# Establecer bits a transmitir en 11 a partir de dos qubits
qc.x(data)
qc.measure(data, data_c)
qc.barrier()

# Aplicar Z y X condicionalmente para encodear 2 bits en un qubit entrelazado
with qc.if_test((data_c[0], 1)):
    qc.z(entangledpair[0])
with qc.if_test((data_c[1], 1)):
    qc.x(entangledpair[0])
qc.barrier()

# Aplicar CNOT con primer qubit como control y segundo como target
qc.cx(entangledpair[0], entangledpair[1])
qc.barrier()

# Aplicar H sobre primer qubit para quitar entrelazamiento
qc.h(entangledpair[0])
qc.barrier()

# Medir ambos qubits
qc.measure(entangledpair[0], entangledpair_c[0])
qc.measure(entangledpair[1], entangledpair_c[1])
qc.barrier()

res = run_circuit(qc)

print(qc.draw())
counts = res.get_counts()

measure_eq_11 = 0
measure_neq_11 = 0
for key in counts:
    if key[-2:] == "11":
        measure_eq_11 += counts[key]
    else:
        measure_neq_11 += counts[key]

print("Probabilidad de recibir 11 en los qubits entrelazados: ", measure_eq_11 / (measure_eq_11 + measure_neq_11))

                                    ░ ┌───┐┌─┐    ░                                                                          ░       ░       ░        ░
                 data_0: ───────────░─┤ X ├┤M├────░──────────────────────────────────────────────────────────────────────────░───────░───────░────────░─
                                    ░ ├───┤└╥┘┌─┐ ░                                                                          ░       ░       ░        ░
                 data_1: ───────────░─┤ X ├─╫─┤M├─░──────────────────────────────────────────────────────────────────────────░───────░───────░────────░─
                         ┌───┐      ░ └───┘ ║ └╥┘ ░        ┌──────┐        ┌───┐┌───────┐      ┌──────┐      ┌───┐┌───────┐  ░       ░ ┌───┐ ░ ┌─┐    ░
       parentrelazado_0: ┤ H ├──■───░───────╫──╫──░────────┤ If-0 ├────────┤ Z ├┤ End-0 ├──────┤ If-0 ├──────┤ X ├┤ End-0 ├──░───■───░─┤ H ├─░─┤M├────░─
                         └───┘┌─┴─┐ ░       ║  ║  ░        └──╥───┘        └───┘└───────┘      └──╥───┘      └───┘└───────┘  ░ ┌─┴─┐ ░ └───┘ ░ └╥┘┌─┐ ░
       parentrelazado_1: ─────┤ X ├─░───────╫──╫──░───────────╫───────────────────────────────────╫──────────────────────────░─┤ X ├─░───────░──╫─┤M├─░─
                              └───┘ ░       ║  ║  ░ ┌─────────╨─────────┐               ┌─────────╨─────────┐                ░ └───┘ ░       ░  ║ └╥┘ ░
          dataclasica: 2/═══════════════════╩══╩════╡ dataclasica_0=0x1 ╞═══════════════╡ dataclasica_1=0x1 ╞═══════════════════════════════════╬══╬════
                                            0  1    └───────────────────┘               └───────────────────┘                                   ║  ║
parentrelazadoclasico: 2/═══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩════
                                                                                                                                                0  1
Probabilidad de recibir 11 en los qubits entrelazados:  1.0