Amplificación de amplitudes

La amplificación de amplitudes puede interpretarse como una primitiva cuántica, es decir como un algoritmo que se abstrae de la implementación y que es reutilizable en otros algoritmos. Por ejemplo, el algoritmo de Grover lo utiliza para un problema de búsqueda en particular.

Objetivo

La amplificación de amplitudes busca generalizar el algoritmo de Grover, preservando la mejora cuadrática y permitiendo la búsqueda sobre un conjunto de elementos no estructurado sin las restricciones impuestas por el mismo. De esta manera, no necesariamente los elementos deben disponerse en una superposición uniforme, y puede haber ninguna, una o varias soluciones. Además, la amplificación de amplitudes pretende funcionar correctamente incluso cuando se desconoce la cantidad de soluciones de antemano.

Solución

Si el espacio de búsqueda posee $N$ elementos, es posible poner el foco sobre su índice, el cual puede enumerarse desde $0$ hasta $N - 1$. Así, se asume la igualdad $N = 2^n$ de manera que el índice pueda ser almacenado en $n$ bits. A su vez, el problema puede tener $M$ soluciones, con $0 \leq M \leq N$. Una instancia del problema de búsqueda puede ser representada por una función $\chi$, que toma un entero $x$ como entrada dentro del rango que va desde $0$ hasta $N - 1$. Por definición, $\chi(x) = 1$ si $x$ es la solución del problema, y $\chi(x) = 0$ en caso contrario.

El algoritmo de amplificación de amplitudes se divide en tres partes: la preparación, la selección y el reflejo.

Figura (1): Estructura de la primitiva de amplificación de amplitudes (AA), con superposición uniforme y que selecciona al estado $\ket{0011}$.

Preparación

La etapa de preparación denota una precondición del algoritmo: que el estado cuántico se encuentre en superposición. La forma en la que será implementada dependerá del problema en cuestión. Generalmente, se habla de un algoritmo cuántico $\mathcal{A}$ que no realiza mediciones durante su ejecución.

El resultado de aplicar dicho algoritmo sobre el estado inicial es el siguiente:

$$\ket{\Psi} = \mathcal{A}\ket{0}$$

Selección

En la etapa de selección, se provee un circuito que distingue los estados cuánticos a buscar. Esto se hace mediante la modificación de la fase de los estados “buenos”, es decir, que conforman una solución. Para ello, se acude a la función $\chi$ antes definida.

En el ejemplo provisto en la figura 1, se implementa con una puerta CZ, marcando el estado $\ket{0011}$, por lo que solo se invertirá la fase para dicho estado. Normalmente se utilizan subrutinas más complejas para invertir las fases. Por ejemplo, en ciertos algoritmos esta etapa se implementa utilizando un oráculo de fase, como ocurre en el algoritmo de Grover.

Reflejo

Finaliza con la etapa de reflejo, que en ciertas bibliografías se lo llama operador de difusión (Grover) o inversión sobre la media (Nielsen y Chuang). Se convierten las diferencias de fases en contrastes de magnitud y se deselecciona los estados marcados en el paso previo.

Iteración

El proceso de amplificación se realiza mediante la aplicación repetida de las etapas de selección y reflejo sobre el estado resultante de la etapa de preparación. Cada iteración comprende la aplicación del siguiente operador unitario:

$$Q = Q(\mathcal{A}, \chi) = -\mathcal{A} S_0 \mathcal{A}^\dag S_{\chi}$$

Donde $S_{\chi}$ cambia condicionalmente el signo de las amplitudes de los estados buenos, $S_{0}$ cambia el signo de la amplitud si y sólo si el estado es $\ket{0}$, y $\mathcal{A}$ representa un algoritmo cuántico que no realiza mediciones durante su ejecución y, por lo tanto, posee inversa.

Análisis

Para evaluar el comportamiento del algoritmo se definen dos conjuntos de cadenas.

$$X_0 = \{x \in \Sigma^n: \chi(x) = 0\}\\ X_1 = \{x \in \Sigma^n: \chi(x) = 1\}$$

El conjunto $X_1$ contiene todas las soluciones del problema de búsqueda, mientras que $X_0$ contiene aquellas cadenas que no son soluciones. Ambos conjuntos satisfacen $X_0 \cap X_1 = \varnothing$ y $X_0 \cup X_1 = \Sigma^n$, lo cual significa que $X_0$ y $X_1$ constituyen una bipartición de $\Sigma^n$ (todas las cadenas de bits de longitud $n$).

Además, se definen dos vectores unitarios que representan los estados de superposición sobre los conjuntos previamente tratados.

$$\ket{\Psi_0} = \sum_{x:\chi(x)=0} a_x \ket{x}\\ \ket{\Psi_1} = \sum_{x:\chi(x)=1} a_x \ket{x}$$

Donde $\ket{\Psi_0}$ equivale al estado de superposición de aquellas cadenas que no son soluciones, mientras que $\ket{\Psi_1}$ constituye la superposición de las cadenas que sí lo son. Estos vectores se encuentran definidos únicamente cuando ninguno de los conjuntos es vacío.

Además, $a = \bra{\Psi_1}\ket{\Psi_1} \ll 1$ es la probabilidad de que la medición de $\ket{\Psi}$ produzca un estado bueno. Así, $1-a = \bra{\Psi_0}\ket{\Psi_0}$ es la probabilidad de que la misma medición produzca un estado malo.

Dado que $\ket{\Psi}$ contiene el estado de superposición inicial sobre todas las cadenas, se cumple la siguiente igualdad:

$$\ket{\Psi} = \mathcal{A}\ket{0} = \ket{\Psi_0} + \ket{\Psi_1}$$

Por lo tanto, $\ket{\Psi}$ representa el estado del programa tras la acción de la etapa de preparación. Esto implica que justo antes de alcanzar la etapa de selección, dicho estado se encuentra contenido en un espacio vectorial abarcado por $\ket{\Psi_0}$ y $\ket{\Psi_1}$. Siempre se tendrá esta propiedad luego de cualquier cantidad de iteraciones al encontrarse en el primer paso de la etapa de reflejo.

También considerar que la Amplificación de Amplitudes no se preocupa sobre cuáles cadenas son soluciones, solamente debe ser capaz de distinguirlas respecto de aquellas cadenas que no lo son.

El operador $Q$ definido previamente puede reescribirse como $Q = U_{\Psi} U_{\Psi_0}$, tales que $U_{\Psi} = 2\ket{\Psi}\bra{\Psi} - I$ y $U_{\Psi_0} = \frac{2}{1-a}\ket{\Psi_0}\bra{\Psi_0} - I$, donde $U_{\Psi_0}$ aplica un reflejo en relación al vector de las no soluciones $\ket{\Psi_0}$ y $U_{\Psi}$ refleja respecto del vector $\ket{\Psi}$.

Visión matricial

Se aplicará $Q$ sobre la base ortonormalizada $\left\{\ket{\psi_0}, \ket{\psi_1}\right\}$ tal que:

$$\ket{\psi_0} = \frac{\ket{\Psi_0}}{\sqrt{1-a}}, \ket{\psi_1} = \frac{\ket{\Psi_1}}{\sqrt{a}}$$

Notar que se cumple la siguiente igualdad:

$$\ket{\Psi} = \ket{\Psi_0} + \ket{\Psi_1} = \sqrt{1-a} \ket{\psi_0} + \sqrt{a} \ket{\psi_1}$$

Al aplicar $Q$ sobre $\ket{\psi_0}$ se obtiene $(1-2a)\ket{\psi_0} + 2\sqrt{a(1-a)} \ket{\psi_1}$.

Cálculo

Al aplicar $Q$ sobre $\ket{\psi_1}$ se obtiene $-2\sqrt{a(1-a)}\ket{\psi_0} + (1-2a)\ket{\psi_1}$.

Cálculo

Por conveniencia, se expresará la acción de $Q$ en un espacio de dos dimensiones como una matriz.

$$M = \begin{pmatrix} 1-2a&-2\sqrt{a(1-a)}\\ 2\sqrt{a(1-a)}&1-2a\\ \end{pmatrix}$$

donde la primera y segunda fila corresponden a $\ket{\psi_0}$ y $\ket{\psi_1}$ respectivamente. Dicha matriz $M$ se obtiene al multiplicar por sí misma una matriz más simple.

$$M = \begin{pmatrix} \sqrt{1-a}&-\sqrt{a}\\ \sqrt{a}&\sqrt{1-a}\\ \end{pmatrix}^2$$

Cálculo

Además, la matriz

$$\begin{pmatrix} \sqrt{1-a}&-\sqrt{a}\\ \sqrt{a}&\sqrt{1-a}\\ \end{pmatrix}$$

es de rotación, la cual puede expresarse como

$$\begin{pmatrix} cos(\theta_a)&-sen(\theta_a)\\ sen(\theta_a)&cos(\theta_a)\\ \end{pmatrix}$$

para $\theta_a = sen^{-1}\left(\sqrt{a}\right) = cos^{-1}\left(\sqrt{1-a}\right)$. Utilizando esta nueva expresión:

$$M = \begin{pmatrix} cos(\theta_a)&-sen(\theta_a)\\ sen(\theta_a)&cos(\theta_a) \end{pmatrix}^2 = \begin{pmatrix} cos(2\theta_a)&-sen(2\theta_a)\\ sen(2\theta_a)&cos(2\theta_a) \end{pmatrix}$$

ya que rotar por el ángulo $\theta_a$ dos veces es equivalente a rotar por el ángulo $2\theta_a$.

Visión geométrica

El estado del programa al comienzo de la primera iteración, tras la etapa de preparación es:

$$\ket{\Psi} = \sqrt{1-a} \ket{\psi_0} + \sqrt{a} \ket{\psi_1} = cos(\theta_a) \ket{\psi_0} + sin(\theta_a) \ket{\psi_1}$$

y el efecto de aplicar $Q$ sobre dicho estado consiste en aplicar una rotación por el ángulo $2\theta_a$ dentro del espacio abarcado por $\ket{\psi_0}$ y $\ket{\psi_1}$.

Por ejemplo:

$$Q^1\ket{\Psi} = cos(3\theta_a) \ket{\psi_0} + sen(3\theta_a) \ket{\psi_1}\\ Q^2\ket{\Psi} = cos(5\theta_a) \ket{\psi_0} + sen(5\theta_a) \ket{\psi_1}\\ Q^3\ket{\Psi} = cos(7\theta_a) \ket{\psi_0} + sen(7\theta_a) \ket{\psi_1}$$

Regla general:

$$Q^k\ket{\Psi} = cos((2k+1)\theta_a) \ket{\psi_0} + sen((2k+1)\theta_a) \ket{\psi_1}$$

La idea es que las iteraciones roten el estado vectorial hacia $\ket{\psi_1}$. Cuando esto ocurre, una medición del estado produce con alta probabilidad una de las salidas superpuestas en $\ket{\psi_1}$, es decir, una solución al problema.

Inicialmente el estado vectorial es ortogonal respecto de $\ket{\psi_1}$. Partiendo de este punto, la operación $U_{\Psi_0}$ refleja el estado en torno a $\ket{\psi_0}$, y luego la operación $U_{\Psi}$ lo refleja en torno a $\ket{\Psi}$. Dado que dos reflexiones producen una rotación, el vector de estado se acerca hacia $\ket{\psi_1}$, y luego de reiteradas rotaciones es posible obtener una solución con alta probabilidad mediante una observación en la base computacional.

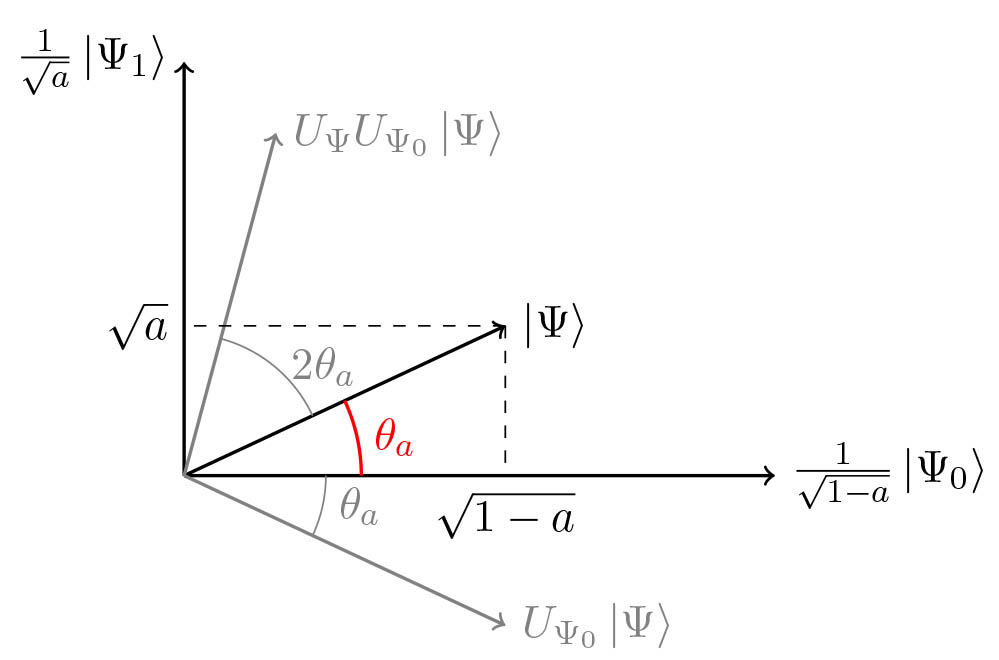
Figura (2): Rotación realizada por el operador $Q$ como composición de dos reflexiones. Fuente: https://alexandre01.github.io/projects/quantum_ampl_estimation/

Complejidad

Sea $a$ la probabilidad inicial de alcanzar una solución a partir de $\mathcal{A}$. Asumiendo $a > 0$ (existe al menos una solución), y definiendo $t = \left\lfloor \frac{\pi}{4\theta_a} \right\rfloor$, donde $\theta_a$ se define tal que $sen^2(\theta_a) = a$ y $0 \lt \theta_a \leq \frac{\pi}{2}$. Entonces, si se computa $Q^t \mathcal{A} \ket{0}$ (se aplica el operador $Q$ $t$ veces) y se realiza una medición, la salida será buena con probabilidad de al menos $max(1 - a, a)$, definida como el valor más grande entre $1 - a$ y $a$.

De esta manera, el número óptimo de iteraciones es el siguiente:

$$N_{iteraciones}= \left\lfloor \frac{\pi}{4}\sqrt{\frac{1}{a}} \right\rfloor = \left\lfloor \frac{\pi}{4}\sqrt{\frac{2^n}{s}} \right\rfloor$$

Donde $n$ es la cantidad de cubits y $s$ es la cantidad de soluciones posibles. En caso de que $a$ se desconozca, es posible recurrir a algunas técnicas para resolver el problema conservando la aceleración cuadrática.

Nota

Realizar más iteraciones de las necesarias puede resultar contraproducente ya que, si se excede el número óptimo de iteraciones $\left(N_{iteraciones} +1\right)$, el estado cúantico permanecerá seleccionado haciendo que la operación de selección funcione de manera insensata.

Demostración

Solución única

Se harán los cálculos necesarios para el caso en el que solamente hay una cadena $x$ tal que $\chi(x) = 1$. Esto quiere decir que $s = 1$.

$$a = \frac{s}{N} = \frac{1}{N}\\ \theta_a = sen^{-1}\left(\sqrt{a}\right) = sen^{-1}\left(\sqrt{\frac{1}{N}}\right)$$

Cuyo valor puede aproximarse a $\sqrt{\frac{1}{N}}$ cuando $N$ es un valor grande.

Sustituyendo el valor $\theta_a = \sqrt{\frac{1}{N}}$ en la expresión $t = \left\lfloor\frac{\pi}{4\theta_a}\right\rfloor$ se obtiene

$$t = \left\lfloor\frac{\pi}{4\theta_a}\right\rfloor = \left\lfloor\frac{\pi}{4N^{-1/2}}\right\rfloor = \left\lfloor\frac{\pi}{4}\sqrt{N}\right\rfloor$$

En base al resultado obtenido en $t$, este caso requiere a lo sumo $O(\sqrt{N})$ consultas para encontrar la solución. La probabilidad de que la medición final resulte en la solución puede expresarse como

$$p(N,1)=sen^2((2t+1)θ))$$

Y en general se cumple

$$p(N,1) >= 1 - \frac{1}{N}$$

para todo $N$, por lo que la probabilidad de éxito tiende a 1 a medida que $N$ crece.

Múltiples soluciones

Se harán los cálculos necesarios para el caso en el que hayan distintas cadenas $x_i$ tal que $\chi(x_i) = 1$.

A medida que la cantidad de elementos en $X_1$ varía, también lo hace el ángulo $\theta_a$, lo cual puede repercutir en gran medida en la probabilidad de éxito del algoritmo. Teniendo $s$ soluciones, habrá que usar el siguiente ángulo:

$$\theta_a=sen^{−1}\left(\sqrt{\frac{s}{N}}\right)$$

y $p(N,s)$ denota la probabilidad del algoritmo para que en $t$ iteraciones encuentre una de las $s$ soluciones dentro de $N$ posibilidades. Puede probarse que

$$p(N,s)\geq 1−\frac{s}{N}$$

y también que

$$p(N,s)\geq \frac{s}{N}$$

Para todo valor $\alpha \in \{0,1\}$ se cumple que $sen^{-1}(\alpha)\geq\alpha$, por lo que puede afirmarse la siguiente inecuación:

$$\theta_a = sen^{-1}(\sqrt{a}) = sen^{-1}\left(\sqrt{\frac{s}{N}}\right) \geq \sqrt{\frac{s}{N}}$$

lo cual implica que

$$t \leq \frac{\pi}{4\theta_a} \leq \frac{\pi}{4} \sqrt{\frac{N}{s}}$$

Por lo tanto, se reduce la cantidad de consultas requeridas a la función $\chi$ a medida que $s$ aumenta. El número de consultas requeridas es de $O\left(\sqrt{\frac{N}{s}}\right)$.

Número desconocido de soluciones

Si el número de soluciones $s = |X_1|$ se desconoce debe implementarse una estrategia para encontrar soluciones con alta probabilidad. Existen diferentes alternativas que serán mencionadas a continuación.

La primera opción consiste en elegir un valor aleatorio de $t$ ubicado entre 1 y $\left\lfloor\frac{\pi}{4}\sqrt{N}\right\rfloor$. De esta manera es posible encontrar una solución (asumiendo que al menos una existe) con una probabilidad mayor al 40%. Si bien esta probabilidad es baja, repitiendo este procedimiento y verificando el resultado puede alcanzarse una solución con una probabilidad muy cercana a 1.

Por otro lado, existe un método que encuentra una solución cuando al menos una existe realizando $O\left(\sqrt{\frac{N}{s}}\right)$ consultas, incluso cuando el número de soluciones de $s$ no es conocido. Cabe destacar que se requieren $O\left(\sqrt{N}\right)$ consultas para determinar que no hay soluciones cuando $s=0$. La idea consiste en elegir $t$ de manera uniforme y aleatoria dentro del conjunto $\{1,...,T\}$ iterativamente, incrementando el valor de $T$. Una estrategia válida es comenzar con $T=1$ e incrementar dicho valor exponencialmente, siempre terminando este proceso tan pronto como una solución sea encontrada y dejando de incrementar $T$ para no desperdiciar consultas cuando ya se sabe que no existe una solución. Este procedimiento tiene la ventaja de que requiere menos consultas cuando hay más soluciones. No obstante, debe tenerse cuidado a la hora de elegir la tasa de crecimiento de $T$: está comprobado que utilizar $T \leftarrow \left\lceil \frac{5}{4}T \right\rceil$ funciona correctamente, pero duplicar $T$ en cada iteración es demasiado agresivo y genera incrementos demasiado rápidos.

Casos triviales

Si todas las cadenas $x \in \Sigma^n$ son una solución, entonces cualquier medición reflejará una solución; y cuando no haya soluciones, ninguna medición obtendrá una solución. El hecho de que $X_0$ o $X_1$ sean vacíos implica que $\chi$ es una función constante: $X_1$ es vacío cuando $\chi(x) = 0$ para todo $x \in \Sigma^n$ y $X_0$ es vacío cuando $\chi(x) = 1$ para todo $x \in \Sigma^n$.

Lo anterior implica que

$$S_{\chi}\ket{\Psi} = \pm\ket{\Psi}$$

y por lo tanto

$$Q\ket{\Psi}=(2\ket{\Psi}\bra{\Psi}-I)S_{\chi}\ket{\Psi}=\pm(2\ket{\Psi}\bra{\Psi}-I)\ket{\Psi}=\pm\ket{\Psi}$$

En conclusión, sin importar la cantidad de iteraciones $t$ que se realicen en estos casos, las mediciones siempre reflejarán una cadena aleatoria $x\in\Sigma^n$.

Ejemplos

Sean $x_1=0001$ y $x_2=0011$ las soluciones a un problema que recurre a la superposición uniforme $\mathcal{A} = H$, se prepara el circuito para distinguir ambas soluciones en la fase de selección. Se sabe de antemano que el problema tiene dos soluciones.

Círculos

Se analizan los pasos del algoritmo donde:

• $\Gamma_0$ es el estado inicial $\ket{0}$
• $\Gamma_1$ se corresponde con la preparación del estado cuántico que resulta en $\ket{\Psi}$
• $\sigma$ representa el resultado de aplicar la operación de selección
• $\lambda$ es el efecto de la etapa de reflejo

En $\sigma$ y $\lambda$ se utilizará como subíndice el número de iteración.

La cantidad óptima de iteraciones es:

$$N_{iteraciones}=\left\lfloor \frac{\pi}{4}\sqrt{\frac{2^4}{2}} \right\rfloor=\left\lfloor \frac{\pi}{4}\sqrt{8} \right\rfloor = 2$$

\(\Gamma_0\)

El estado inicial del algoritmo $\ket{0}^{\otimes 4}$

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\Gamma_1\)

Estado cuántico luego de la preparación (aplicación del algoritmo $\mathcal{A} = H$)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\sigma_1\)

Notar que $\ket{x_1}$ y $\ket{x_2}$ tienen invertida la fase

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_1\)

Notar la “deselección” de $\ket{0011}$ y $\ket{0001}$

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\sigma_2\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_2\)

Notar que no “deselecciona” ya que alcanzó la cantidad óptima de iteraciones.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Llegados a este punto, el problema se encuentra resuelto con una probabilidad de 96.875%, ya que las probabilidades individuales de obtener $\ket{x_1}$ o $\ket{x_2}$ son de 47.2656%, y sumadas dan la probabilidad total de llegar a una solución. Se realiza una tercera iteración para mostrar el decremento de la probabilidad al exceder la cantidad óptima de iteraciones.

\(\sigma_3\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_3\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Por lo que en una tercera iteración se disminuyen las probabilidades de encontrar una de las soluciones.

Quirk

Nota

La puerta flip_x1/x2 permite seleccionar las soluciones $x_1$ y $x_2$. Es implementada de forma similar a lo diagramado en la Figura (1) durante la etapa de selección, en la cual únicamente se distingue $x_2$. Mientras tanto, mirror es exactamente igual a la etapa de reflejo de dicha figura.

Qiskit

Código

from qiskit import QuantumCircuit, circuit, transpile
from qiskit_aer import QasmSimulator

QUBIT_COUNT = 4
QUBITS = range(QUBIT_COUNT)
ITERATIONS = 2
NUMBERS_TO_FIND = [1, 3]
A = circuit.library.HGate()

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled_qc = transpile(qc)
    result = sim.run(transpiled_qc).result()
    return result

def flip(qc: QuantumCircuit, nums_to_find: list[int]):
    """
    Aplica la operación de selección sobre los números recibidos en 'nums_to_find'.
    Para cada número en 'nums_to_find', esta función voltea su fase.
    Un número N se representa como un estado computacional |N⟩.
    """
    for num in nums_to_find:
        # Determine the qubits that need an X gate to transform |num⟩ to |1...1⟩.
        # These are the qubits that are '0' in the binary representation of num.
        # Qiskit's convention: q0 is LSB.
        # Example: num=1 (0001 for 4 qubits), X applied to q1, q2, q3.
        # Example: num=3 (0011 for 4 qubits), X applied to q2, q3.

        qubits_to_apply_x = []
        for i in range(QUBIT_COUNT):
            # Check if the i-th bit of num (from LSB) is 0
            if not (num & (1 << i)):
                qubits_to_apply_x.append(i)

        # Apply X gates to transform |num⟩ to |1...1⟩
        if qubits_to_apply_x:
            qc.x(qubits_to_apply_x)

        # Apply multi-controlled Z gate (MCZ) to flip the phase of |1...1⟩.
        # ZGate().control(N-1) applied to N qubits acts as an MCZ gate
        # that flips the phase of the state |1⟩^{otimes N}.
        if QUBIT_COUNT > 0:
            mcz_gate = circuit.library.ZGate().control(QUBIT_COUNT - 1)
            qc.append(mcz_gate, QUBITS)

        # Apply X gates again to transform back from |1...1⟩ to |num⟩
        if qubits_to_apply_x:
            qc.x(qubits_to_apply_x)

    return qc

def mirror(qc: QuantumCircuit):
    """
    Aplica el operador espejo al circuito cuántico
    También llamado operador de difusión de Grover
    Utilizando el algoritmo de superposición A
    """
    for qubit_idx in QUBITS:
        qc.append(A, [qubit_idx])

    qc.x(QUBITS)

    if QUBIT_COUNT > 0:
        mcz_gate = circuit.library.ZGate().control(QUBIT_COUNT - 1)
        qc.append(mcz_gate, QUBITS)

    qc.x(QUBITS)

    for qubit_idx in QUBITS:
        qc.append(A, [qubit_idx])

    return qc

def analyze_aa_results(results):
    counts = results.get_counts()
    print("Resultados (counts):", counts)

    # Calculate total shots for percentages
    total_shots = sum(counts.values())
    if total_shots == 0:
        print("Porcentajes: No shots found.")
        return

    # Calculate percentages
    # Qiskit measurement string is MSB first, e.g., '0001' for 4 qubits.
    # This corresponds to decimal 1.
    percentages = {}
    for bitstring, count in counts.items():
        decimal_value = int(bitstring, 2)
        percentages[decimal_value] = (count / total_shots) * 100

    ordered_percentages = dict(sorted(percentages.items(), key=lambda item: item[1], reverse=True))

    print("Porcentajes (ordenados):")
    for val, perc in ordered_percentages.items():
        binary_representation = format(val, f'0{QUBIT_COUNT}b')
        print(f"  Estado |{binary_representation}⟩ (Decimal {val}): {perc:.2f}%")


# Create Quantum Circuit
qc = QuantumCircuit(QUBIT_COUNT, QUBIT_COUNT)

# 1. Initialize state to uniform superposition: H^{otimes n} |0...0⟩
for qubit_idx in QUBITS:
    qc.append(A, [qubit_idx])

# 2. Iterations
for iteration in range(ITERATIONS):
    qc.barrier()
    # Apply phase flip for solutions
    qc = flip(qc, NUMBERS_TO_FIND)
    qc.barrier()
    # Apply Diffusion operator (mirror)
    qc = mirror(qc)
    qc.barrier()

# 3. Measurement
qc.measure(QUBITS, QUBITS)

# Print the circuit
print("Diagrama del circuito cuántico:")
print(qc.draw(output='text'))

# Run the circuit and analyze results
print("
Ejecutando el circuito...")
results = run_circuit(qc)
analyze_aa_results(results)

Resultado

Diagrama del circuito cuántico:
     ┌───┐ ░                            ░ ┌───┐┌───┐   ┌───┐┌───┐ ░  ░                            ░ ┌───┐┌───┐   ┌───┐┌───┐ ░ ┌─┐
q_0: ┤ H ├─░───────■────────────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──░───────■────────────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░─┤M├─────────
     ├───┤ ░ ┌───┐ │ ┌───┐      │       ░ ├───┤├───┤ │ ├───┤├───┤ ░  ░ ┌───┐ │ ┌───┐      │       ░ ├───┤├───┤ │ ├───┤├───┤ ░ └╥┘┌─┐
q_1: ┤ H ├─░─┤ X ├─■─┤ X ├──────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──░─┤ X ├─■─┤ X ├──────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──╫─┤M├──────
     ├───┤ ░ ├───┤ │ ├───┤┌───┐ │ ┌───┐ ░ ├───┤├───┤ │ ├───┤├───┤ ░  ░ ├───┤ │ ├───┤┌───┐ │ ┌───┐ ░ ├───┤├───┤ │ ├───┤├───┤ ░  ║ └╥┘┌─┐
q_2: ┤ H ├─░─┤ X ├─■─┤ X ├┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──░─┤ X ├─■─┤ X ├┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──╫──╫─┤M├───
     ├───┤ ░ ├───┤ │ ├───┤├───┤ │ ├───┤ ░ ├───┤├───┤ │ ├───┤├───┤ ░  ░ ├───┤ │ ├───┤├───┤ │ ├───┤ ░ ├───┤├───┤ │ ├───┤├───┤ ░  ║  ║ └╥┘┌─┐
q_3: ┤ H ├─░─┤ X ├─■─┤ X ├┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──░─┤ X ├─■─┤ X ├┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░──╫──╫──╫─┤M├
     └───┘ ░ └───┘   └───┘└───┘   └───┘ ░ └───┘└───┘   └───┘└───┘ ░  ░ └───┘   └───┘└───┘   └───┘ ░ └───┘└───┘   └───┘└───┘ ░  ║  ║  ║ └╥┘
c: 4/══════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩══╩══╩═
                                                                                                                               0  1  2  3

Ejecutando el circuito...
Resultados (counts): {'1110': 1, '0000': 2, '0001': 492, '1111': 5, '0011': 483, '0111': 1, '1011': 2, '1100': 4, '0010': 5, '0100': 3, '1001': 4, '0101': 6, '1000': 6, '0110': 3, '1101': 3, '1010': 4}
Porcentajes (ordenados):
  Estado |0001⟩ (Decimal 1): 48.05%
  Estado |0011⟩ (Decimal 3): 47.17%
  Estado |0101⟩ (Decimal 5): 0.59%
  Estado |1000⟩ (Decimal 8): 0.59%
  Estado |1111⟩ (Decimal 15): 0.49%
  Estado |0010⟩ (Decimal 2): 0.49%
  Estado |1100⟩ (Decimal 12): 0.39%
  Estado |1001⟩ (Decimal 9): 0.39%
  Estado |1010⟩ (Decimal 10): 0.39%
  Estado |0100⟩ (Decimal 4): 0.29%
  Estado |0110⟩ (Decimal 6): 0.29%
  Estado |1101⟩ (Decimal 13): 0.29%
  Estado |0000⟩ (Decimal 0): 0.20%
  Estado |1011⟩ (Decimal 11): 0.20%
  Estado |1110⟩ (Decimal 14): 0.10%
  Estado |0111⟩ (Decimal 7): 0.10%

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 6, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Libro

Capítulo 7.6.3, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Libro

Capítulo 6.1.2, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Video

Grover's Algorithm | Understanding Quantum Information & Computation - Lesson 08 (Qiskit) [Inglés]

Paper

Quantum Amplitude Amplification and Estimation (Gilles Brassard; Peter Høyer; Michele Mosca; Alain Tapp) [Inglés]

Paper

A fast quantum mechanical algorithm for database search (Lov K. Grover) [Inglés]