Algoritmo de Grover

El algoritmo de Grover es el algoritmo de búsqueda cuántico por excelencia, ya que permite encontrar un elemento dentro de un conjunto de elementos no estructurado. Es muy importante porque puede aplicarse sobre diferentes clases de problemas y acelerar los algoritmos clásicos que usan heurísticas de búsqueda.

Objetivo

Dada una base de datos no ordenada de $N$ elementos, de la cual sólo uno de ellos satisface una propiedad en particular, se quiere encontrar dicho elemento. El mejor algoritmo clásico conocido realiza esta tarea en $O(N)$ pasos, mientras que este algoritmo puede resolverlo en $O(\sqrt{N})$ pasos.

Solución

Los pasos llevados a cabo en este algoritmo se corresponden con la metodología general de la amplificación de amplitudes (AA), implementada de manera específica para el problema planteado en este artículo. Se recomienda ver la explicación completa de dicha primitiva y luego volver para comprender su aplicación sobre el algoritmo de Grover. Cabe aclarar que, a diferencia de lo expuesto en AA, el circuito utilizará un cubit auxiliar adicional para implementar el oráculo de fase.

Preparación

El programa comienza en el estado $\ket{0}^{\otimes n}$ (ignorando cubits auxiliares). El algoritmo de Grover recurre a la superposición $\mathcal{A} = H$, aplicando la transformación de Hadamard para alcanzar un estado de superposición uniforme sobre todas las soluciones en el espacio de búsqueda.

$$\ket{\Psi} = \mathcal{A}\ket{0} = H\ket{0} = \frac{1}{\sqrt N} \sum_{0}^{N - 1}\ket{x}$$

Selección

La función $\chi$, encargada de reconocer la solución al problema, se asume implementada por medio de un oráculo cuántico. Precisamente, se trata de un oráculo de fase, encargado de marcar la solución del problema de búsqueda aplicando un cambio de fase. En este artículo se llamará $O$ al operador asociado a dicho oráculo. En términos de AA, $S_{\chi} = O$.

Reflejo

Se produce a efectos de la puerta Hadamard ya que se trabaja con superposiciones uniformes.

Iteración

Las iteraciones de Grover son comprendidas por las etapas de selección y reflejo. Sean $S_{\chi} = O$, $\mathcal{A} = H$ y $\mathcal{A}^\dag = H$ debido a que la transformación de Hadamard es su propia inversa. En términos de AA, las iteraciones de Grover constituyen la aplicación del siguiente operador $Q$:

$$Q = -H S_0 H O$$

Complejidad

Dado que la probabilidad inicial de éxito $a$ es exactamente $\frac{1}{N}$ (existe una única solución al problema), si se mide luego de $m = \left\lfloor \frac{\pi}{4} \sqrt{N} \right\rfloor$ iteraciones de $Q$, la probabilidad de encontrar la solución tiene una cota inferior de $1 - \frac{1}{N}$. Ver detalles en AA.

Circuito

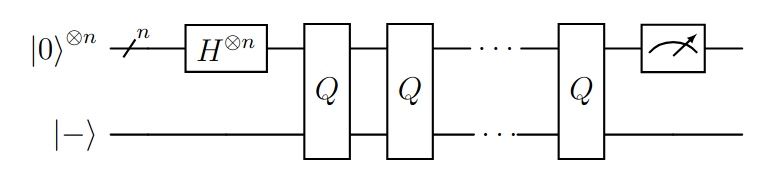
Figura (1): Algoritmo de Grover en un circuito cuántico utilizando la iteración de Grover $Q$.

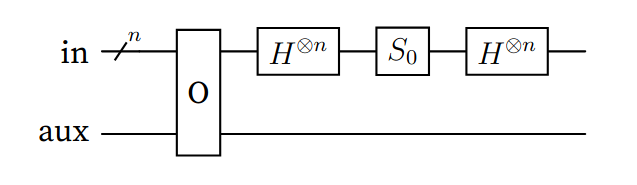
Figura (2): Iteración de Grover Q en un circuito cuántico. “In” representa el estado del registro de búsqueda, mientras que “aux” es el cubit auxiliar usado por el oráculo de fase.

Ejemplos

Sea $x=0011$ la solución única al problema, se modifica el oráculo con una función que toma valor 1 únicamente con dicha cadena. Se sabe de antemano que el problema tiene una solución.

Círculos

Se analizan los pasos del algoritmo donde:

• $\Gamma_0$ es el estado inicial $\ket{0}$
• $\Gamma_1$ se corresponde con la preparación del estado cuántico que resulta en $\ket{\Psi}$
• $\sigma$ representa el resultado de aplicar la operación de selección
• $\lambda$ es el efecto de la etapa de reflejo

En $\sigma$ y $\lambda$ se utilizará como subíndice el número de iteración.

La cantidad óptima de iteraciones es:

$$N_{iteraciones}=\left\lfloor \frac{\pi}{4}\sqrt{\frac{2^4}{1}} \right\rfloor=\lfloor \pi \rfloor = 3$$

\(\Gamma_0\)

El estado inicial del algoritmo $\ket{0}^{\otimes 4}$

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\Gamma_1\)

Estado cuántico luego de la preparación (aplicación del algoritmo $\mathcal{A} = H$)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\sigma_1\)

Notar que $\ket{0011}$ tiene invertida la fase

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_1\)

Notar la “deselección” de $\ket{0011}$

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\sigma_2\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_2\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\sigma_3\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_3\)

Notar que no “deselecciona” ya que alcanzó la cantidad óptima de iteraciones.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Llegados a este punto, el problema se encuentra resuelto con una probabilidad de 96.1319%. Se realiza una cuarta iteración para mostrar el decremento de la probabilidad al exceder la cantidad óptima de iteraciones.

\(\sigma_4\)

Notar que la operación de “selección” no logró distinguir al estado bueno.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

\(\lambda_4\)

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Por lo que en una cuarta iteración se disminuyen las probabilidades de encontrar el número buscado.

Quirk

Nota

El cubit más significativo (desde abajo hacia arriba en el circuito) es el auxiliar utilizado por el oráculo O, el cual permite seleccionar la solución $x$. Mientras tanto, mirror está diagramada como la etapa de reflejo de la Figura (1) del artículo de AA.

Qiskit

Código

from qiskit import QuantumCircuit, circuit, transpile
from qiskit_aer import QasmSimulator

QUBIT_COUNT = 4
QUBITS = range(QUBIT_COUNT)
ITERATIONS = 3
NUMBER_TO_FIND = 3

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled).result()
    return result

def flip(qc, num):
    """
    Aplica la operación de dar vuelta un numero al circuito cuántico
    Selecciona `num` como el elemento marcado
    """
    x_bits = ~num
    x_list = [x for x in range(QUBIT_COUNT) if x_bits & (1 << x)]
    qc.x(x_list)
    cz_gate = circuit.library.ZGate().control(QUBIT_COUNT-1)
    qc.append(cz_gate, QUBITS)
    qc.x(x_list)

    return qc

def mirror(qc):
    """
    Aplica el operador espejo al circuito cuántico
    También llamado operador de difusión de Grover
    """
    qc.h(QUBITS)
    qc.x(QUBITS)
    cz_gate = circuit.library.ZGate().control(QUBIT_COUNT-1)
    qc.append(cz_gate, QUBITS)
    qc.x(QUBITS)
    qc.h(QUBITS)
    return qc

def analyze_results(results):
    counts = results.get_counts()
    print("Resultados:", counts)
    total = sum(counts.values())
    percentages = {key: f"{value / total*100:.2f}%" for key, value in counts.items()}
    ordered_percentages = dict(sorted(percentages.items(), key=lambda item: item[1], reverse=True))
    print("Porcentajes:", ordered_percentages)

qc = QuantumCircuit(QUBIT_COUNT, QUBIT_COUNT)
qc.h(QUBITS)

for _ in range(ITERATIONS):
    qc.barrier()
    qc = flip(qc, NUMBER_TO_FIND)
    qc.barrier()
    qc = mirror(qc)

qc.measure(QUBITS, QUBITS)
print(qc.draw())

res = run_circuit(qc)
analyze_results(res)

Resultado

     ┌───┐ ░               ░ ┌───┐┌───┐   ┌───┐┌───┐ ░               ░ ┌───┐┌───┐   ┌───┐┌───┐ ░               ░ ┌───┐┌───┐   ┌───┐┌───┐┌─┐
q_0: ┤ H ├─░───────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░───────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░───────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├┤M├─────────
     ├───┤ ░       │       ░ ├───┤├───┤ │ ├───┤├───┤ ░       │       ░ ├───┤├───┤ │ ├───┤├───┤ ░       │       ░ ├───┤├───┤ │ ├───┤├───┤└╥┘┌─┐
q_1: ┤ H ├─░───────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░───────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░───────■───────░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─╫─┤M├──────
     ├───┤ ░ ┌───┐ │ ┌───┐ ░ ├───┤├───┤ │ ├───┤├───┤ ░ ┌───┐ │ ┌───┐ ░ ├───┤├───┤ │ ├───┤├───┤ ░ ┌───┐ │ ┌───┐ ░ ├───┤├───┤ │ ├───┤├───┤ ║ └╥┘┌─┐
q_2: ┤ H ├─░─┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░─┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░─┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─╫──╫─┤M├───
     ├───┤ ░ ├───┤ │ ├───┤ ░ ├───┤├───┤ │ ├───┤├───┤ ░ ├───┤ │ ├───┤ ░ ├───┤├───┤ │ ├───┤├───┤ ░ ├───┤ │ ├───┤ ░ ├───┤├───┤ │ ├───┤├───┤ ║  ║ └╥┘┌─┐
q_3: ┤ H ├─░─┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░─┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─░─┤ X ├─■─┤ X ├─░─┤ H ├┤ X ├─■─┤ X ├┤ H ├─╫──╫──╫─┤M├
     └───┘ ░ └───┘   └───┘ ░ └───┘└───┘   └───┘└───┘ ░ └───┘   └───┘ ░ └───┘└───┘   └───┘└───┘ ░ └───┘   └───┘ ░ └───┘└───┘   └───┘└───┘ ║  ║  ║ └╥┘
c: 4/════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩══╩══╩═
                                                                                                                                         0  1  2  3
Resultados: {'1111': 1, '1101': 2, '0100': 1, '0000': 2, '0010': 2, '1001': 4, '1100': 2, '0101': 3, '1110': 3, '1010': 3, '0111': 4, '0011': 997}
Porcentajes: {'0011': '97.36%', '1001': '0.39%', '0111': '0.39%', '0101': '0.29%', '1110': '0.29%', '1010': '0.29%', '1101': '0.20%', '0000': '0.20%', '0010': '0.20%', '1100': '0.20%', '1111': '0.10%', '0100': '0.10%'}

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 7.6.3, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Libro

Capítulo 6, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Video

Grover's Algorithm | Understanding Quantum Information & Computation - Lesson 08 (Qiskit) [Inglés]

Otros

How the quantum search algorithm works (Quantum Country) [Inglés]

Libro

Capítulo 10, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Paper

A fast quantum mechanical algorithm for database search (Lov K. Grover) [Inglés]