Algoritmo de Deutsch-Jozsa

El algoritmo de Deutsch-Jozsa es uno de los algoritmos más conocidos en la rama cuántica. Es uno de los primeros algoritmos cuánticos que surgieron, y baja notablemente la cota temporal respecto de la mejor alternativa clásica conocida. Este mismo motivó a la creación de los algoritmos más famosos como el de Shor o el de Grover, entre muchos más.

Objetivo

El algoritmo permite determinar si una función $f$ es constante o balanceada. Una función es constante cuando $f$ ante cualquier entrada retorna siempre la misma salida, es decir siempre retorna $0$ o siempre retorna $1$. Por otra parte la función es balanceada cuando retorna mitad de veces una salida y mitad de veces otra, es decir retorna $n/2$ veces $0$ y $1$ respectivamente.

El algoritmo clásico, implica recorrer, en el peor de los casos, al menos mitad de las salidas posibles ( $2^{n-1}+1$ ). El algoritmo cuántico realiza esta operación en una sola pasada.

Deutsch

Se plantea en un principio una versión reducida del problema, llamado problema de Deutsch, donde la función que se evalúa es binaria:

f: \{0,1\} \rightarrow \{0,1\}

Esto permite simplificar el algoritmo en su unidad más básica, permitiendo que se comprenda el problema que el algoritmo resuelve. Posteriormente se explicará la versión completa del algoritmo de Deutsch-Jozsa para una función de mayor complejidad.

Solución

El siguiente circuito resuelve el problema de Deutsch para una función binaria:

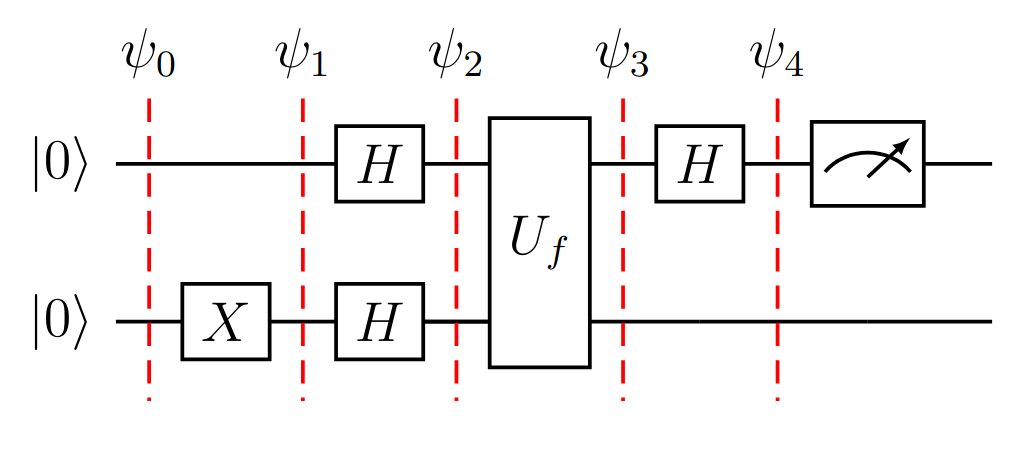
Algoritmo Deutsch en un circuito con separadores ante la aplicación de cada puerta.

Figura (1): Algoritmo de Deutsch en un circuito con separadores ante la aplicación de cada puerta.

En este circuito cuántico se utilizan las puertas Pauli X, Hadamard y un oráculo $U_f$ que es un oráculo de fase. Notar que el oráculo de fase se encuentra asociado a $f$, que es la función que se quiere determinar si es constante o balanceada.

A continuación se analiza paso a paso el estado de los cubits según los separadores provistos en el grafico, donde $\psi_i$ es el estado en el paso $i$, empezando con $i=0$ y finalizando con $i=4$:

\begin{align} \psi_0=&\ket{00}\\ \psi_1=&\ket{10}\\ \psi_2=&\ket{-+}\\ \psi_3=&\frac{1}{\sqrt{2}}((-1)^{f(0)}\ket{0}+(-1)^{f(1)}\ket{1})\\ \psi_4=& \begin{cases} H\ket{+}=\ket{0} & \text{si \(f(0)=f(1)\)}\\ H\ket{-}=\ket{1} & \text{si \(f(0) \neq f(1)\)} \end{cases} \end{align}

La idea básica del algoritmo es poder reemplazar $U_f$ con un circuito. Si este circuito representa una función constante, la salida del primer cubit será $\ket{0}$ . En caso de que el circuito represente una función balanceada, retornará $\ket{1}$ .

Desarrollo elaborado

De forma detallada el estado de los cubits según los separadores provistos en la Figura 1, donde $\psi_i$ es el estado en el paso $i$, empezando con $i=0$ y finalizando con $i=4$:

\begin{align} \psi_0=&\ket{00}\\ \psi_1=&\ket{10}\\ \psi_2=&\ket{-+}\\ =&\frac{1}{\sqrt{2}}(\ket{-}\ket{0}+\ket{-}\ket{1})\\ \psi_3=&U_f\frac{1}{\sqrt{2}}(\ket{-}\ket{0}+\ket{-}\ket{1})\\ =&\frac{1}{\sqrt{2}}(U_f\ket{-}\ket{0}+U_f\ket{-}\ket{1})\\ =&\frac{1}{\sqrt{2}}((-1)^{f(0)}\ket{-}\ket{0}+(-1)^{f(1)}\ket{-}\ket{1})\\ =&\frac{1}{\sqrt{2}}((-1)^{f(0)}\ket{0}+(-1)^{f(1)}\ket{1})\\ \end{align}

Notar que se elimina el cubit $\ket-$. Esto se debe a que no se mide ni se utiliza más en el circuito, por lo que solo estorbaría y por ende se puede omitir.

Se analizan los casos posibles. Primero en caso de que $f$ sea constante, y luego en caso de que $f$ sea balanceada.

\begin{align} =&\begin{cases} \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})=\ket{+} & \text{si \(f(0)=f(1)=0\)}\\ \frac{1}{\sqrt{2}}(-\ket{0}-\ket{1})=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})=\ket{+} & \text{si \(f(0)=f(1)=1\)} \end{cases}\\ =&\begin{cases} \frac{1}{\sqrt{2}}(\ket{0}-\ket{1})=\ket{-} & \text{si \(f(0)=0, f(1)=1\)}\\ \frac{1}{\sqrt{2}}(-\ket{0}+\ket{1})=\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})=\ket{-} & \text{si \(f(0)=1, f(1)=0\)} \end{cases} \end{align}

A su vez se factoriza el $-1$ que, como actúa de fase global, se puede descartar.

Finalmente, aplicar el último paso del circuito es simple.

\begin{align} \psi_4= \begin{cases} H\ket{+}=\ket{0} & \text{si \(f(0)=f(1)\)}\\ H\ket{-}=\ket{1} & \text{si \(f(0) \neq f(1)\)} \end{cases} \end{align}

Ejemplos

En estos ejemplos se definirán circuitos que representan tanto funciones constantes como balanceadas. Estos circuitos reemplazarán el oráculo definido previamente que abstraía la función a analizar.

Funciones Constantes

Un circuito que no posee puertas cuánticas permite representar una función constante $f$ , cuya definición se corresponde con $f(x)=0$ para cualquier valor recibido como entrada (en este caso, $0$ o $1$ ).

Circuito con dos cubits, siendo el primero la entrada de la función y el segundo su correspondiente salida. Denota una función constante donde f(x)=0.

Figura (2): Circuito con dos cubits, siendo el primero la entrada de la función y el segundo su correspondiente salida. Denota una función constante donde $f(x)=0$ .

Notar que si $x=0$ (primer cubit en el circuito de la izquierda), el resultado de la función $f(x)$ (segundo cubit) es $0$ , y de la misma manera si $x=1$ (circuito de la derecha) la salida de $f(x)$ sigue siendo $0$ , es decir que $f(0)=f(1)=0$ .

Si se introduce esta función/circuito dentro del algoritmo de Deutsch, la salida debe ser $\ket{0}$ . Gráficamente se observaría de la siguiente manera:

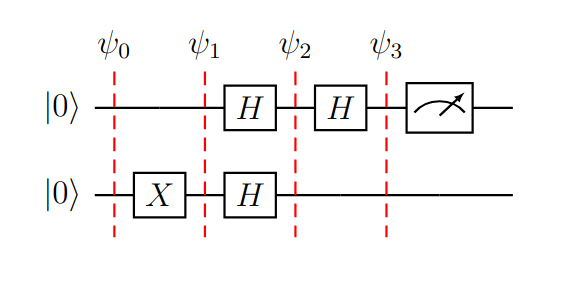
Figura (3): Algoritmo Deutsch en un gráfico con separadores ante la aplicación de cada puerta, utilizando la función constante en vez del oráculo.

Desarrollando paso a paso el estado de los cubits según los separadores provistos:

\begin{align} \psi_0=&\ket{00}\\ \psi_1=&\ket{10}\\ \psi_2=&\ket{-+}\\ \psi_3=&\ket{-0}\\ =&\ket{0}\\ \end{align}

Se elimina el $\ket{-}$ ya que no es utilizado en la medición. Con este resultado se llega rápidamente a que, utilizando una función constante, se deriva correctamente al resultado $\ket{0}$ .

$\psi_0$

El estado inicial del algoritmo $\ket{00}$

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_1$

Aplicación de $X$ sobre el cubit del oráculo.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_2$

Aplicación de puertas Hadamard sobre ambos cubits. Recordar que en este ejemplo el oráculo para $f(x)=0$ es un circuito sin puertas cuánticas.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_3$

Se aplica Hadamard sobre el cubit menos significativo para obtener la respuesta final.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

Ignorando el estado del cubit del oráculo (el cubit más significativo), la probabilidad de obtener $\ket{0}$ es del $100\%$ .

regs = [QuantumRegister(2, "q"), ClassicalRegister(1, "c")]
qc = QuantumCircuit(*regs)
qc.h(0)
qc.x(1)
qc.h(1)
qc.barrier()
# no hace nada
qc.barrier()
qc.h(0)
qc.measure(0, 0)

La función descrita previamente es constante y retorna 0 ante cualquier entrada. Otro ejemplo de función constante es aquella que siempre retorna 1 como salida, la cual puede implementarse aplicando una puerta Pauli-X a la salida.

Funciones Balanceadas

Puede implementarse un circuito que represente una función balanceada mediante la aplicación de una puerta $CNOT$ .

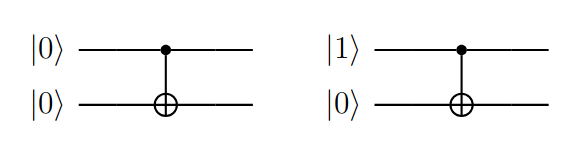
Circuito con dos cubits, siendo el primero la entrada de la función y el segundo su correspondiente salida. Denota una función balanceada

Figura (4): Circuito con dos cubits, siendo el primero la entrada de la función y el segundo su correspondiente salida. Denota una función balanceada.

Notar que si $x=0$ (primer cubit en el circuito de la izquierda), el resultado de la función $f(x)$ (segundo cubit) es $0$ , y si $x=1$ (circuito de la derecha) la salida de $f(x)$ es $1$ , es decir que $f(0)\neq f(1)$ .

Si se introduce esta función/circuito dentro del algoritmo de Deutsch, la salida, a diferencia del previo, debe ser $\ket{1}$ . Gráficamente se observaria de la siguiente manera:

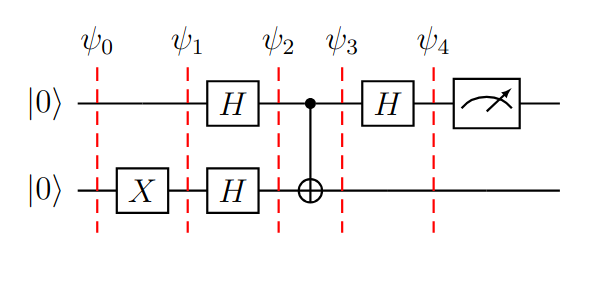
Figura (5): Algoritmo Deutsch en un gráfico con separadores ante la aplicación de cada puerta, utilizando la función balanceada en vez del oráculo.

Desarrollando paso a paso los estados de los cubits en cada separador se obtiene:

\begin{align} \psi_0=&\ket{00}\\ \psi_1=&\ket{10}\\ \psi_2=&\ket{-+}\\ \psi_3=&CNOT\ket{-+}\\ =&\ket{--}\\ \psi_4=&\ket{-1}\\ =&\ket{1} \end{align}

Una derivación del paso $\psi_3$ se puede encontrar en el artículo CNOT. Nuevamente se omite el cubit en estado $\ket{-}$ porque no se utiliza en la medición.

Esto determina que, para una función balanceada, se deriva al resultado correcto. La medición resulta en $\ket{1}$ .

$\psi_0$

El estado inicial del algoritmo $\ket{00}$

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_1$

Aplicación de $X$ sobre el cubit del oráculo.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_2$

Aplicación de puertas Hadamard sobre ambos cubits. Recordar que en este ejemplo el oráculo para función balanceada es un circuito con la puerta $CNOT$ , con el cubit menos significativo como control y el más significativo como objetivo.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_3$

Retroceso de fase mediante la aplicación del oráculo.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

$\psi_4$

Se aplica Hadamard sobre el cubit menos significativo para obtener la respuesta final.

$$\ket{00}$$

$$\ket{01}$$

$$\ket{10}$$

$$\ket{11}$$

Ignorando el estado del cubit del oráculo (el cubit más significativo), la probabilidad de obtener $\ket{1}$ es del $100\%$ .

regs = [QuantumRegister(2, "q"), ClassicalRegister(1, "c")]
qc = QuantumCircuit(*regs)
qc.h(0)
qc.x(1)
qc.h(1)
qc.barrier()
qc.cx(0, 1)
qc.barrier()
qc.h(0)
qc.measure(0, 0)

La función descrita previamente es balanceada, retornando el mismo valor que la entrada (función identidad). Otro ejemplo de función balanceada es aquella que siempre retorna el opuesto de la entrada como salida (función de opuesto). Esta puede implementarse, por ejemplo, aplicando una puerta Pauli-X a la salida luego de haber aplicado $CNOT$ .

Deutsch-Jozsa

El problema que resuelve el algoritmo de Deutsch-Jozsa es la generalización del algoritmo previo para funciones con $n$ entradas de tamaño $n$ .

f: \{0,1\}^n \rightarrow \{0,1\}

Solución

El algoritmo de Deutsch-Jozsa se describe de forma genérica con el siguiente circuito:

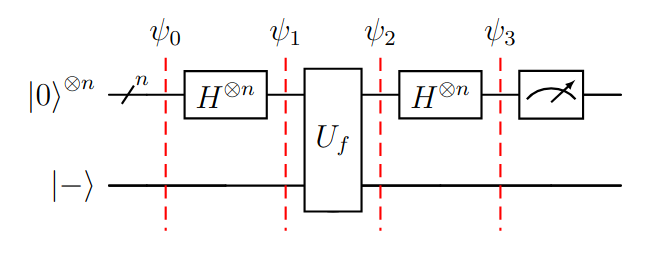
Figura (6): Algoritmo Deutsch-Jozsa en un circuito con separadores ante la aplicación de cada puerta.

Este mantiene una estructura similar al algoritmo de Deutsch planteado en la figura 1, pero con algunos cambios:

Se reemplaza el cubit más significativo de $\ket{0}$ a $\ket{-}$ . Esto es equivalente a aplicar una puerta Pauli-X y Hadamard, pero se evitó para mejorar la legibilidad.
Se generaliza el cubit de entrada a $n$ cubits que representan los valores de entrada. Esto está representado por el símbolo / $^n$ previo a $\psi_0$ .
Se aplican las puertas Hadamard a los $n$ cubits de entrada, y el oráculo es aplicado a los $n$ cubits de entrada y al cubit que de salida de la función.

A continuación se analiza paso a paso el estado de los cubits según los separadores provistos en el gráfico, donde $\psi_i$ es el estado en el paso $i$, empezando con $i=0$ y finalizando con $i=3$:

\begin{align} \psi_0=&\ket{-}\ket{0}^{\otimes n}\\ \psi_1=&\ket{-}H^{\otimes n}\ket{0}^{\otimes n}\\ =&\ket{-}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} \ket{x}\\ \psi_2=&U_f\ket{-}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} \ket{x}\\ =&\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\ket{x}\\ \psi_3=&H^{\otimes n}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\ket{x}\\ =&\sum_{z\in\{0,1\}^n} \left(\frac{1}{2^n}\sum_{x\in\{0,1\}^n} (-1)^{f(x)+x\cdot z}\right) \ket{z}\\ \end{align}

Desarrollo elaborado

Pasos 0 y 1

\begin{align} \psi_0=&\ket{-}\ket{0}^{\otimes n}\\ \psi_1=&\ket{-}H^{\otimes n}\ket{0}^{\otimes n}\\ =&\ket{-}\underbrace{H\ket{0}H\ket{0}\ldots H\ket{0}}_{n\text{ veces}}\\ =&\ket{-}\underbrace{\ket{++\ldots +}}_{n\text{ veces}}\\ =&\ket{-}\underbrace{\frac{\ket{0}+\ket{1}}{\sqrt{2}}\frac{\ket{0}+\ket{1}}{\sqrt{2}}\ldots\frac{\ket{0}+\ket{1}}{\sqrt{2}}}_{n\text{ veces}}\\ \end{align}

Valor de $\psi_1$ en caso de que $n=2$ :

\begin{align} H^{\otimes 2}\ket{0}^{\otimes 2}=&\ket{-}\frac{\ket{0}+\ket{1}}{\sqrt{2}}\frac{\ket{0}+\ket{1}}{\sqrt{2}}\\ =&\frac{1}{\sqrt{2^2}}(\ket{0}+\ket{1})\otimes(\ket{0}+\ket{1})\\ =&\frac{1}{\sqrt{2^2}}(\ket{00}+\ket{01}+\ket{10}+\ket{11})\\ =&\frac{1}{\sqrt{2^2}}\sum_{x \in \{0,1\}^2} \ket{x} \end{align}

Notar que en este caso $\sum_{x \in \{0,1\}^2} \ket{x}$ denota la suma de todas las combinaciones de tamaño $2$ , por lo que el caso general (para $n$ entradas) es el siguiente:

H^{\otimes n}\ket{0}^{\otimes n}=\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n}\ket{x}

Finalmente $\psi_1$ toma el valor:

\psi_1=\ket{-}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n}\ket{x}

Paso 2

\begin{align} \psi_2=&U_f\ket{-}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} \ket{x}\\ =&\ket{-}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} U_f\ket{x}\\ =&\ket{-}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\ket{x}\\ =&\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\ket{x}\\ \end{align}

En el último paso se omite $\ket{-}$ para simplificar los cálculos, ya que no se utiliza en la medición y no interfiere con el resto del algoritmo.

Paso 3

\begin{align} \psi_3=&H^{\otimes n}\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\ket{x}\\ =&\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}H^{\otimes n}\ket{x}\\ \end{align}

Notar que $H^{\otimes n}\ket{x}$ es diferente a $H^{\otimes n}\ket{0}$ definido previamente. Este puede entenderse como:

\begin{align} H^{\otimes n}\ket{x}&=H\ket{x_{n-1}x_{n-2}x_{n-3} \ldots x_0}\\ &=H\ket{x_{n-1}}H\ket{x_{n-2}} \ldots H\ket{x_0}\\ H\ket{x_i}&=\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{x_i}\ket{1})\quad\text{donde }x_i\in\{0,1\} \end{align}

$\psi_3$ cuando $n=2$ :

\begin{align} H^{\otimes 2}\ket{x}&=H\ket{x_1}H\ket{x_0}\\ &=\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{x_1}\ket{1})\frac{1}{\sqrt{2}}(\ket{0}+(-1)^{x_0}\ket{1})\\ &=\frac{1}{\sqrt{2^2}}(\ket{0}+(-1)^{x_1}\ket{1})(\ket{0}+(-1)^{x_0}\ket{1})\\ &=\frac{1}{\sqrt{2^2}}(\ket{00}+(-1)^{x_0}\ket{01}+(-1)^{x_1}\ket{10}+(-1)^{x_1}(-1)^{x_0}\ket{11})\\ &=\frac{1}{\sqrt{2^2}}(\ket{00}+(-1)^{x_0}\ket{01}+(-1)^{x_1}\ket{10}+(-1)^{x_0+x_1}\ket{11})\\ &=\frac{1}{\sqrt{2^2}}(\ket{00}+(-1)^{x\cdot10}\ket{01}+(-1)^{x\cdot 01}\ket{10}+(-1)^{x\cdot 11}\ket{11})\\ &=\frac{1}{\sqrt{2^2}}\sum_{z\in\{0,1\}^2} (-1)^{x\cdot z} \ket{z} \end{align}

Notar que se convierte $x_1$ al producto escalar $x \cdot 01$ para simplificar la ecuación. Dado que la operación $x\cdot 01$ equivale a lo siguiente:

x \cdot 01 = x_0x_1 \cdot 01 = x_0(0) + x_1(1) = x_1

Se puede generalizar la ecuación para $n$ :

H^{\otimes n}\ket{x}=\frac{1}{\sqrt{2^n}}\sum_{z\in\{0,1\}^n} (-1)^{x\cdot z} \ket{z}

Finalmente reemplazando en $\psi_3$ :

\begin{align} \psi_3=&\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}H^{\otimes n}\ket{x}\\ =&\frac{1}{\sqrt{2^n}}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\left[\frac{1}{\sqrt{2^n}}\sum_{z\in\{0,1\}^n} (-1)^{x\cdot z} \ket{z}\right]\\ =&\sum_{x\in\{0,1\}^n}\frac{1}{2^n} (-1)^{f(x)}\left[\sum_{z\in\{0,1\}^n} (-1)^{x\cdot z} \ket{z}\right]\\ =&\sum_{x\in\{0,1\}^n}\frac{1}{2^n} \sum_{z\in\{0,1\}^n} (-1)^{f(x)}(-1)^{x\cdot z} \ket{z}\\ =&\sum_{x\in\{0,1\}^n}\frac{1}{2^n} \sum_{z\in\{0,1\}^n} (-1)^{f(x)+x\cdot z} \ket{z}\\ =&\sum_{z\in\{0,1\}^n} \left(\frac{1}{2^n}\sum_{x\in\{0,1\}^n} (-1)^{f(x)+x\cdot z}\right) \ket{z}\\ \end{align}

La identidad definida previamente $H^{\otimes n}\ket{0}^{\otimes n}$ se puede generalizar utilizando la identidad definida con $H^{\otimes n}\ket{x}$ , donde $\ket{x}=\ket{0}^{\otimes n}$ :

\begin{align} H^{\otimes n}\ket{0}^{\otimes n}&=H^{\otimes n}\ket{00\ldots 0}\\ H^{\otimes n}\ket{00\ldots 0}&=\frac{1}{\sqrt{2^n}}\sum_{z\in\{0,1\}^n}(-1)^{00\ldots 0\cdot z} \ket{z}\\ &=\frac{1}{\sqrt{2^n}}\sum_{z\in\{0,1\}^n}(-1)^0 \ket{z}\\ &=\frac{1}{\sqrt{2^n}}\sum_{z\in\{0,1\}^n}\ket{z} \end{align}

Finalmente si se mide la amplitud del estado $\psi_3$ donde $\ket{z}$ es $\ket{0}^{\otimes{n}}$

\begin{gather} \left|\frac{1}{2^n}\sum_{x\in\{0,1\}^n} (-1)^{f(x)+x\cdot 00\ldots 0}\right|^2=\left|\frac{1}{2^n}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\right|^2\\ \end{gather}

Cálculo

Estas amplitudes convergen en diferentes resultados según si $f$ es constante o balanceada. Por un lado, si es constante:

\begin{align} \left|\frac{1}{2^n}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\right|^2=1 \end{align}

Cálculo

Por otro lado, si es balanceada:

\begin{align} \left|\frac{1}{2^n}\sum_{x\in\{0,1\}^n} (-1)^{f(x)}\right|^2=0 \end{align}

Cálculo

Ahora, a diferencia del algoritmo previo, se puede reemplazar $U_f$ con un circuito que represente una función constante o una función balanceada con $n$ entradas. En caso de ser del primer tipo la probabilidad de medir $\ket{0}^{\otimes n}$ es $1$ , y en caso de ser del segundo tipo la probabilidad de medir $\ket{0}^{\otimes n}$ es $0$ .

Ejemplos

Sea $f$ una función con 3 entradas y una salida, se debe codificar este oráculo en el circuito del algoritmo de Deutsch-Jozsa.

Función constante
Función balanceada

$\psi_0$

Estado inicial del algoritmo $\ket{-000}$

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

$\psi_1$

Aplicación de puertas Hadamard sobre los tres cubits menos significativos. Recordar que en este ejemplo el oráculo para $f(x)=0$ es un circuito sin puertas cuánticas.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

$\psi_2$

Aplicación del oráculo. Recordar que en este ejemplo el oráculo para $f(x)=0$ es un circuito sin puertas cuánticas, por lo que no hay cambios en el estado.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

$\psi_3$

Se aplica Hadamard sobre los cubits que no son del oráculo (todos excepto el más significativo). Así se obtiene la respuesta final.

$$\ket{0000}$$

$$\ket{0001}$$

$$\ket{0010}$$

$$\ket{0011}$$

$$\ket{0100}$$

$$\ket{0101}$$

$$\ket{0110}$$

$$\ket{0111}$$

$$\ket{1000}$$

$$\ket{1001}$$

$$\ket{1010}$$

$$\ket{1011}$$

$$\ket{1100}$$

$$\ket{1101}$$

$$\ket{1110}$$

$$\ket{1111}$$

Ignorando el estado del cubit del oráculo (el cubit más significativo), la probabilidad de obtener $\ket{000}$ es del $100\%$ .

from qiskit import QuantumCircuit
from qiskit_aer import QasmSimulator
from qiskit import transpile

def run_circuit(qc: QuantumCircuit):
    sim = QasmSimulator()
    transpiled = transpile(qc)
    result = sim.run(transpiled).result()
    return result

def circuit_deutsch_jozsa(function: QuantumCircuit):
    """
    Compila un circuito para usarlo en el algoritmo de Deutsch-Jozsa.
    """
    n = function.num_qubits - 1
    qc = QuantumCircuit(n + 1, n)
    qc.x(n)
    qc.h(range(n + 1))
    qc.compose(function, inplace=True)
    qc.h(range(n))
    qc.measure(range(n), range(n))
    return qc

def dj_function(num_inputs):
    """
    Crea una función de Deutsch-Jozsa aleatoria (balanceada/constante).
    - num_qubits: el número de entradas de la función
    """

    qc = QuantumCircuit(num_inputs + 1)
    qc.barrier()
    if np.random.rand() > 0.5:
        qc.x(num_inputs)
    else:
        qc.cx(0, num_inputs)
    qc.barrier()
    return qc


def analyze_dj_results(results):
    """
    Analiza los resultados de una ejecución de Deutsch-Jozsa.
    Determina si la función es constante o balanceada segun los resultados.
    """
    counts = results.get_counts()
    # obtiene la medición del primer qubit (el de arriba)
    key = list(counts.keys())[0]
    if key[-1] == "0":
        return key + ": constante"
    else:
        return key + ": balanceada"


num_inputs = 3
if len(sys.argv) >= 2:
    num_inputs = int(sys.argv[1]) # permite cambiar la cantidad de entradas
oracle = dj_function(num_inputs) # crea una función constante/balanceada
print("Oráculo:")
print(oracle.draw())
print("Circuito Deutsch-Jozsa:")
dj_circuit = circuit_deutsch_jozsa(oracle) # codifica el oráculo en el circuito
print(dj_circuit.draw())
print("Corriendo el circuito de Deutsch-Jozsa:")
print(analyze_dj_results(run_circuit(dj_circuit)))

Oráculo:
      ░       ░
q_0: ─░───────░─
      ░       ░
q_1: ─░───────░─
      ░       ░
q_2: ─░───────░─
      ░ ┌───┐ ░
q_3: ─░─┤ X ├─░─
      ░ └───┘ ░
Circuito Deutsch-Jozsa:
     ┌───┐      ░       ░ ┌───┐┌─┐
q_0: ┤ H ├──────░───────░─┤ H ├┤M├──────
     ├───┤      ░       ░ ├───┤└╥┘┌─┐
q_1: ┤ H ├──────░───────░─┤ H ├─╫─┤M├───
     ├───┤      ░       ░ ├───┤ ║ └╥┘┌─┐
q_2: ┤ H ├──────░───────░─┤ H ├─╫──╫─┤M├
     ├───┤┌───┐ ░ ┌───┐ ░ └───┘ ║  ║ └╥┘
q_3: ┤ X ├┤ H ├─░─┤ X ├─░───────╫──╫──╫─
     └───┘└───┘ ░ └───┘ ░       ║  ║  ║
c: 3/═══════════════════════════╩══╩══╩═
                                0  1  2
Corriendo el circuito de Deutsch-Jozsa:
000: constante

Oráculo:
      ░       ░
q_0: ─░───■───░─
      ░   │   ░
q_1: ─░───┼───░─
      ░   │   ░
q_2: ─░───┼───░─
      ░ ┌─┴─┐ ░
q_3: ─░─┤ X ├─░─
      ░ └───┘ ░
Circuito Deutsch-Jozsa:
     ┌───┐      ░       ░ ┌───┐┌─┐
q_0: ┤ H ├──────░───■───░─┤ H ├┤M├──────
     ├───┤      ░   │   ░ ├───┤└╥┘┌─┐
q_1: ┤ H ├──────░───┼───░─┤ H ├─╫─┤M├───
     ├───┤      ░   │   ░ ├───┤ ║ └╥┘┌─┐
q_2: ┤ H ├──────░───┼───░─┤ H ├─╫──╫─┤M├
     ├───┤┌───┐ ░ ┌─┴─┐ ░ └───┘ ║  ║ └╥┘
q_3: ┤ X ├┤ H ├─░─┤ X ├─░───────╫──╫──╫─
     └───┘└───┘ ░ └───┘ ░       ║  ║  ║
c: 3/═══════════════════════════╩══╩══╩═
                                0  1  2
Corriendo el circuito de Deutsch-Jozsa:
001: balanceada

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 7.3.3, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Video

Deutsch's Algorithm: An Introduction to Quantum Computing Oracles (Quantum Soar) [Inglés]

Video

Deutsch-Jozsa Algorithm: Exponential Speedup on a Quantum Computer! (Quantum Soar) [Inglés]

Video

Quantum Query Algorithms | Understanding Quantum Information & Computation - Lesson 05 (Qiskit) [Inglés]

Otros

Quantum Computing (CST Part II) | Lecture 7: Deutsch-Jozsa algorithm (Cambridge) [Inglés]

Libro

Capítulo 1.4.3 y 1.4.4, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Paper

Analysis of Deutsch-Jozsa Quantum Algorithm (Zhengjun Cao; Lihua Liu) [Inglés]

Video

Deutsch Jozsa Algorithm - Quantum Computer Programming w/ Qiskit p.3 (sentdex) [Inglés]