Descomputación

Existen ocasiones en las que el procesamiento cuántico produce cubits “basura”. Esto puede afectar los resultados de cómputo debido a que los bits basura, cuyo valor depende del estado de entrada, generalmente destruirán las propiedades de interferencia que son tan importantes para la computación cuántica. Por ejemplo, podría requerirse trabajar con el entrelazamiento y el mismo se efectuaría con cubits que se encuentran en estados inservibles. Es por esto que en estos casos es buena práctica aplicar descomputación, una técnica que permite dejar los cubits auxiliares en $\ket{0}$ para que no interfieran durante el entrelazamiento. La idea consiste en revertir las operaciones que entrelazaron los cubits basura, retornándolos a su estado inicial $\ket{0}$, con un pequeño costo en el tiempo de procesamiento.

A continuación se explicará el funcionamiento de esta técnica, aplicada sobre un ejemplo de procesamiento cuántico.

El proceso de descomputación involucra tres pasos:

• Computar $\ket{0}\ket{0}\ket{x} \rightarrow \ket{w(x)}\ket{s(x)}\ket{x}$, donde $x$ es el estado inicial, $s(x)$ el resultado de aplicar una operación sobre $x$ y $w(x)$ el estado “basura” resultante tras haber ejecutado $s(x)$. Se utiliza el enfoque estándar que consiste en convertir puertas clásicas $AND$ y $NOT$ en puertas cuánticas $Toffoli$ y $NOT$, respectivamente.
• Agregar un cubit extra en el estado $\ket{0}$, y aplicar la puerta $CNOT$ sobre $\ket{s(x)}$ como el control. Esto permitirá copiar el resultado y se obtendrá: $\ket{s(x)}\ket{w(x)}\ket{s(x)}\ket{x}$
• Ahora aplicar todas las puertas del primer paso pero en orden inverso, y aplicando en cada paso la puerta inversa. El resultado deshará lo ocurrido en el paso 1, resultando en $\ket{s(x)}\ket{0}\ket{0}\ket{x}$

Se puede ignorar el estado $\ket{0}\ket{0}$, el cual no es modificado durante todo el proceso. Así, el resultado de estos pasos es la transformación deseada:

$$\ket{0}\ket{x} \rightarrow \ket{s(x)}\ket{x}$$

Resumiendo, si se tiene un circuito clásico para computar una función $s(\cdot)$, se puede pensar en las tres etapas del circuito cuántico limpio como: computar $s(\cdot)$, convirtiendo puertas clásicas en cuánticas; copiar la respuesta usando $CNOT$; y finalmente aplicar descomputación, revirtiendo las puertas e invirtiéndolas.

Suponiendo que se intenta computar $s(x) = x_1 \land x_2 \land x_3$, es decir, la operación $AND$ de tres bits, se usará una puerta $Toffoli$ para computar el $AND$ de los primeros dos bits, $x_1 \land x_2$:

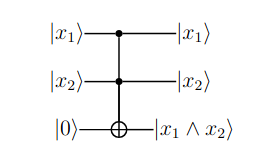
Figura (1): Operación $AND$ sobre $x_1$ y $x_2$ usando puertas $Toffoli$

Luego se usaría otra puerta $Toffoli$ para aplicar la operación $AND$ entre el resultado de la operación previa y $x_3$:

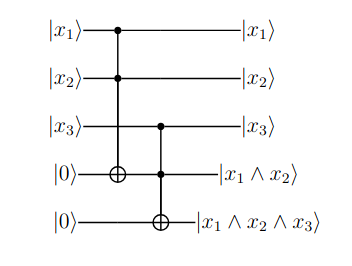
Figura (2): Operación $AND$ entre el resultado previo y $x_3$ usando puertas $Toffoli$

Hasta este punto se ha computado $s(x) = x_1 \land x_2 \land x_3$, pero durante el proceso se ha generado también un cubit intermedio en el estado $\ket{x_1 \land x_2}$. Este estado no era parte de la especificación original.

Se quería computar

$$\ket{0}\ket{x_3, x_2, x_1} \rightarrow \ket{x_1 \land x_2 \land x_3}\ket{x_3, x_2, x_1}$$

pero se terminó computando

$$\ket{0}\ket{0}\ket{x_3, x_2, x_1} \rightarrow \ket{x_1 \land x_2 \land x_3}\ket{x_1 \land x_2}\ket{x_3, x_2, x_1}$$

Esto puede evitarse fácilmente aplicando descomputación. Siguiendo los pasos mencionados previamente, y recordando que la puerta $Toffoli$ es inversa de sí misma:

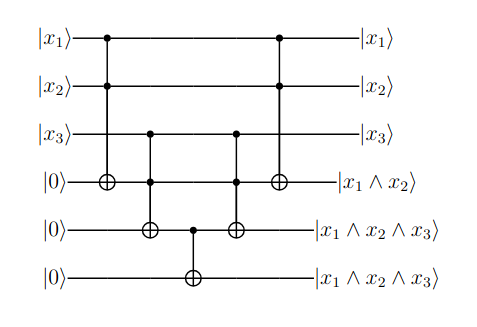
Figura (3): Aplicación de descomputación sobre la operación $x_1 \land x_2 \land x_3$ usando puertas $Toffoli$

El costo de aplicar descomputación es lineal en relación a los números de cubits involucrados en el circuito, ya que deben aplicarse las operaciones inversas a las utilizadas inicialmente. Además, el número de cubits auxiliares escala a lo sumo linealmente para guardar los resultados de las operaciones intermedias. Por lo tanto, es posible aplicar descomputación sobre los circuitos de forma eficiente, utilizando dicha práctica cuando sea requerida con el objetivo de mantener estados de cómputo limpios.

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Otros

How the quantum search algorithm works (Quantum Country) [Inglés]

Libro

Capítulo 5, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Libro

Capítulo 4.5.2, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Libro

Capítulo 3.2.5, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]