El Cubit

En la computación clásica existe el bit como la unidad mínima de información. Análogamente, en la computación cuántica se adoptó el término cubit (quantum bit) para referirse a la unidad mínima de información propia de este paradigma. Los cubits pueden describirse como objetos matemáticos que tienen ciertas propiedades particulares. Así como un bit tiene un estado (0 o 1), un cubit también lo tiene. Dos estados posibles son $\ket{0}$ y $\ket{1}$, los cuales se corresponden con los estados 0 y 1 de un bit clásico. La diferencia principal entre los bits y los cubits radica en que estos últimos pueden estar en otros estados, ya que es posible formar combinaciones lineales de estados, conocidas como superposiciones:

$$\ket{\psi} = \alpha \ket{0} + \beta \ket{1}$$

Donde los números $\alpha$ y $\beta$ son números complejos, aunque en muchos casos basta con interpretarlos como números reales. Dicho de otra manera, el estado de un cubit es un vector en un espacio vectorial complejo de dos dimensiones. Los estados $\ket{0}$ y $\ket{1}$ son conocidos como estados computacionales base, y forman una base ortonormal para este espacio vectorial.

Una particularidad de los cubits consiste en que no es posible examinarlos para determinar su estado cuántico, es decir, sus valores de $\alpha$ y $\beta$. Cuando se mide un cubit se obtiene el valor 0 con probabilidad $|\alpha|^2$ o el valor 1 con probabilidad $|\beta|^2$. Debe cumplirse que $|\alpha|^2 + |\beta|^2 = 1$, ya que las probabilidades deben sumar 1 en total. Geométricamente esto puede interpretarse como la condición de que el estado del cubit debe ser normalizado a longitud 1. Por lo tanto, generalmente el estado de un cubit es un vector unitario en un espacio vectorial complejo de dos dimensiones.

En base a lo anterior, es posible afirmar que la medición de un cubit retornará únicamente 0 o 1. Además, la medición cambia el estado de un cubit, colapsando su superposición de $\ket{0}$ y $\ket{1}$ a un estado específico que sea consistente con el resultado de la medición.

Para darse una idea de por qué la computación cuántica podría tener un gran potencial, notar que existe un número infinito de superposiciones posibles en las que un solo cubit puede existir previo a ser leído.

Representación de los cubits

Existen diversas formas de representar los estados cuánticos de los cubits, cuya visualización suele ser complementaria y puede facilitar la legibilidad y comprensión en función del problema a tratar.

Una de las notaciones más conocidas es la notación Dirac, también conocida como bra-ket (utiliza los símbolos $\bra{}$ y $\ket{}$). Es la notación estándar para los estados en la mecánica cuántica. Los números encerrados en notación bra-ket denotan valores que un cubit podría tener al momento de ser leído. Por ejemplo:

$$\frac{1}{\sqrt{2}} \ket{0} + \frac{1}{\sqrt{2}} \ket{1}$$

Dado que $|\alpha|^2 + |\beta|^2 = 1$, puede definirse la ecuación anterior como

$$\ket{\psi} = e^{i\gamma} \left( cos\left(\frac{\theta}{2}\right) \ket{0} + e^{i\phi} sin\left(\frac{\theta}{2}\right) \ket{1} \right)$$

donde $\theta$, $\phi$ y $\gamma$ son números reales. Los números $\theta$ y $\phi$ definen un punto en una esfera unitaria de tres dimensiones, que es conocida como esfera de Bloch. Esta provee una manera útil de visualizar el estado de un solo cubit. Sin embargo, aún no se encontró una generalización sencilla de la esfera de Bloch para múltiples cubits.

Siguiendo la convención de la física tradicional, el eje $x$ es el que “sale” de la página, el eje $y$ apunta hacia un costado, y el eje $z$ se encuentra orientado hacia arriba. Por lo tanto, ya que la esfera de Bloch es de radio 1 (de forma que los estados cuánticos se encuentren normalizados), $\ket{0}$ corresponde al punto $(x, y, z) = (0, 0, 1)$, y $\ket{1}$ corresponde al punto $(0, 0, -1)$. Es importante notar que un cubit puede estar en cualquier punto de la esfera de Bloch.

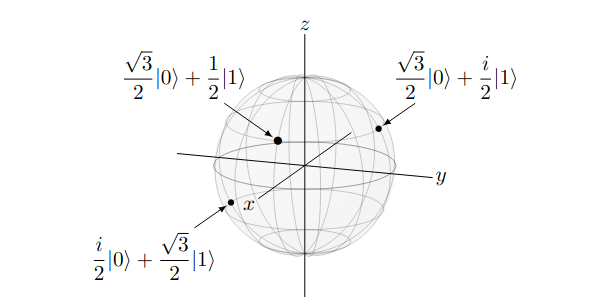
Figura (1): Esfera de Bloch con tres estados cuánticos que representan distintos puntos dentro de la esfera. Fuente: https://www.thomaswong.net/introduction-to-classical-and-quantum-computing-1e4p.pdf

Por otra parte, la notación de círculos ha surgido como una alternativa de visualización interesante. La misma muestra el estado cuántico de la siguiente manera:

• La magnitud de la amplitud asociada con cada valor que un cubit puede tomar ($\ket{0}$ o $\ket{1}$) se encuentra relacionada al radio del área pintada con color expuesta para cada uno de los círculos $\ket{0}$ o $\ket{1}$.
• La fase relativa entre las amplitudes de dichos valores se encuentra indicada por la rotación del círculo $\ket{1}$ relativamente al círculo $\ket{0}$ (se traza una línea oscura en los círculos para que pueda visualizarse dicha rotación).

Figura (2): Notación de círculos, donde cada estado está asociado a dos círculos: el de la izquierda representa al $\ket{0}$ y el de la derecha al $\ket{1}$. El primer estado devolverá $\ket{0}$ con $100\%$ de probabilidad. El segundo estado retornará $\ket{1}$ con $100\%$ de probabilidad. El tercer estado tiene una probabilidad $50:50$ para $\ket{0}$ y $\ket{1}$. El cuarto estado tiene la misma probabilidad que el anterior, con la diferencia de que existe una fase relativa de $180º$ (esto se percibe mediante la línea oscura). El último estado retornará $\ket{0}$ con un $90\%$ de probabilidad.

Por convención, un ángulo positivo rota al círculo en el sentido contrario de las agujas del reloj. Además, suele rotarse únicamente el círculo $\ket{1}$, ya que lo único que importa es la fase relativa entre ambos estados base $\ket{0}$ y $\ket{1}$. No obstante, cabe recalcar que la fase relativa de un cubit no produce efecto alguno sobre las magnitudes en una superposición, por lo que no tiene influencia directa sobre los resultados observables en una medición en la base $\{\ket{0}, \ket{1}\}$.

Otra forma de visualizar al cubit puede emplearse mediante la representación vectorial, donde:

$$\ket{0} = \begin{bmatrix} 1\\ 0 \end{bmatrix}, \ket{1} = \begin{bmatrix} 0\\ 1 \end{bmatrix}$$

Esta quizás es la concepción más cercana al punto de vista matemático, y podría ser de utilidad para algunos casos particulares, donde se facilitarían los cálculos al realizar operaciones con puertas cuánticas, acudiendo a su representación matricial.

Representación de múltiples cubits

A la hora de trabajar con varios cubits puede que ninguna de las representaciones mostradas previamente sean lo ideal debido a que se tornan poco prácticas y, en muchos casos, ilegibles. Es por esto que se desarrollaron los circuitos cuánticos como estrategia de representación de algoritmos y secuencias de aplicación de puertas cuánticas sobre uno o varios cubits que son manipulados a lo largo de su ciclo de vida. Bajo esta representación, las líneas que van de izquierda a derecha representan “cables cuánticos”, donde cada uno de ellos representa a un cubit. El cable cuántico permite visualizar cómo un cubit es sometido a diferentes cambios a lo largo del tiempo, mediante la aplicación de diferentes puertas cuánticas. Cada puerta es representada con un símbolo diferente dentro del circuito. Generalmente, las puertas unarias son representadas como cajas con una etiqueta de texto que indica el tipo de puerta.

Figura (3): Visualización de puertas unitarias A, B y C en un circuito cuántico

Por otro lado, las puertas n-arias se representan mediante una línea que conecta diferentes cubits.

Figura (4): Visualización de puertas binarias Controlled NOT y Controlled Y en un circuito cuántico

La operación de medición es representada por un símbolo de un medidor que siempre recibe un cubit como entrada y genera información clásica como salida (denotada por una línea doble).

Figura (5): Visualización de la medición de un cubit en un circuito cuántico

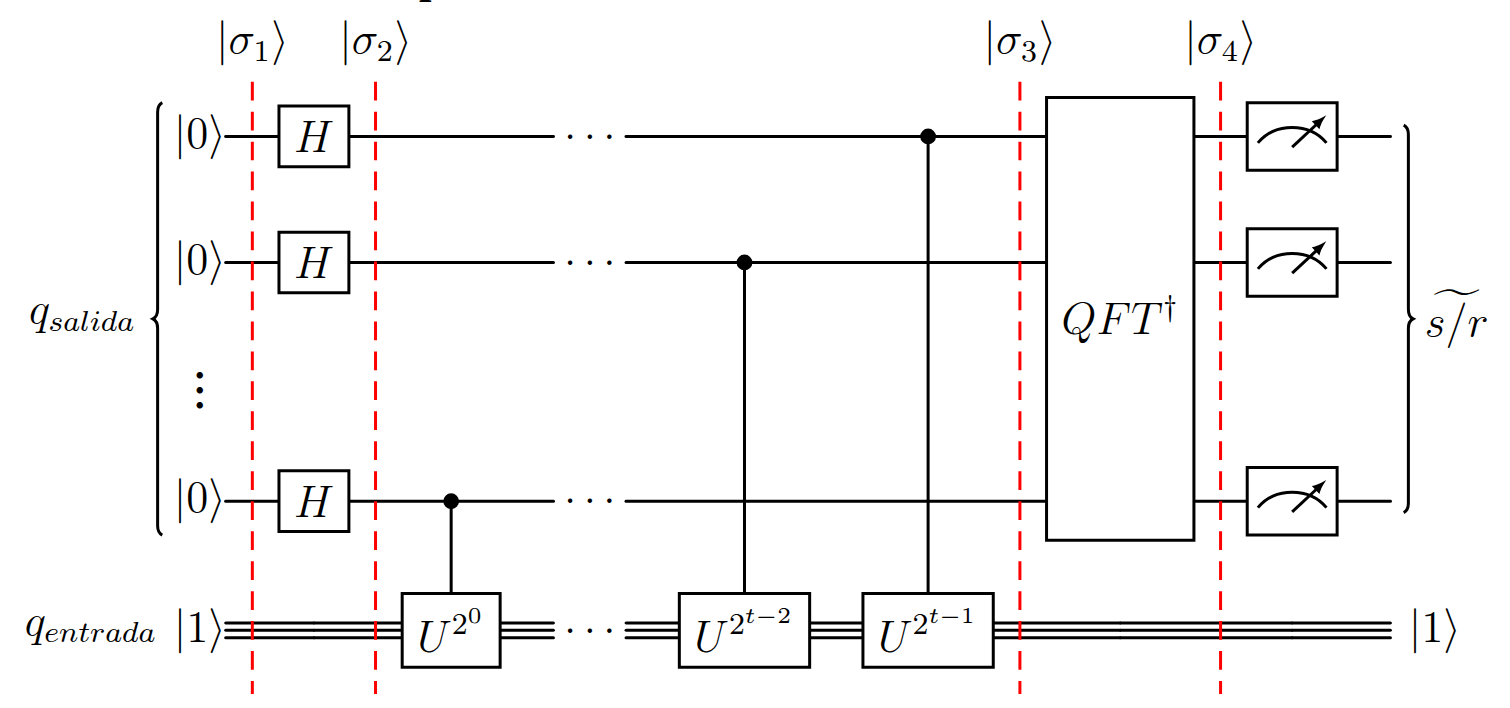
Figura (6): Ejemplo de circuito cuántico, el cual representa la estructura de la primitiva EF aplicada al algoritmo de Shor.

Nota

En Qudos se utiliza la representación Little Endian. Esto quiere decir que el cubit ubicado en la parte superior del circuito será el menos significativo, y el que está debajo de todo es el más significativo. Notará que de acuerdo a la bibliografía esta decisión diferirá. Se optó por utilizar esta arquitectura debido a que es la que se usa con mayor frecuencia, y es la adoptada por Quirk y Qiskit.

Mediciones en otras bases

Dentro de la esfera de Bloch se describió al $\ket{0}$ y $\ket{1}$ como sus polos norte y sur respectivamente. Sin embargo, dos puntos opuestos cualesquiera pueden ser tomados como polos norte y sur. Por ejemplo, $\ket{+}$ y $\ket{-}$ pueden serlo, así como también $\ket{i}$ y $\ket{-i}$, o cualquier otro par de puntos opuestos. Un conjunto de resultados de la medición es llamado una base, y $\{\ket{0}, \ket{1}\}$ es denominada base Z porque acude al eje $Z$ de la esfera de Bloch. De forma similar, $\{\ket{+}, \ket{-}\}$ constituye la base X porque recurre al eje $X$ de la esfera, mientras que $\{\ket{i}, \ket{-i}\}$ es llamada base Y porque acude al eje $Y$ de la misma. Es posible medir respecto a cualquiera de estas bases, o respecto a cualquier par de estados opuestos dentro de la esfera de Bloch.

Fase global y Fase relativa

Cuando se habla de fase, se hace referencia a una rotación. Existen dos tipos de fase: fase global y fase relativa.

Un ejemplo de fase global puede observarse en el siguiente estado:

$$e^{i\theta}\left(\frac{\sqrt{3}}{2}\ket{0} + \frac{1}{2}\ket{1}\right)$$

donde la fase $e^{i\theta}$ se aplica sobre todo el estado cuántico.

Notar que a la hora de realizar una medición la probabilidad de obtener $\ket{0}$ es:

$$\left|e^{i\theta}\frac{\sqrt{3}}{2}\right|^2 = e^{i\theta}e^{-i\theta} \left(\frac{\sqrt{3}}{2}\right)^2 = e^0 \frac{3}{4} = \frac{3}{4}$$

Por otra parte, la probabilidad de obtener $\ket{1}$ es:

$$\left|e^{i\theta}\frac{1}{2}\right|^2 = e^{i\theta}e^{-i\theta} \left(\frac{1}{2}\right)^2 = e^0 \frac{1}{4} = \frac{1}{4}$$

De lo anterior se deduce que para cualquier valor que pueda tomar la fase global, la misma no producirá cambios en las probabilidades de la medición. Por lo tanto, las fases globales son físicamente irrelevantes. Y como tales, pueden ignorarse. Esto se debe a que los estados que difieren únicamente en su fase global son realmente el mismo estado; corresponden al mismo punto en la esfera de Bloch.

Mientras tanto, la fase relativa refleja una rotación de $\ket{1}$ en relación a $\ket{0}$. Este tipo de fase es físicamente importante, ya que dos estados cuánticos con fases relativas diferentes representan dos puntos distintos en la esfera de Bloch, los cuales pueden distinguirse mediante mediciones en las bases apropiadas. Por ejemplo, a partir de los siguientes estados cuánticos:

$$\ket{+} = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1})\\ \ket{i} = \frac{1}{\sqrt{2}}(\ket{0} + i\ket{1}) = \frac{1}{\sqrt{2}}\left(\ket{0} + e^{i\pi/2}\ket{1}\right)$$

Si se aplica una medición en base Z se obtendrán las mismas estadísticas: $\ket{0}$ con probabilidad $1/2$ o $\ket{1}$ con probabilidad $1/2$. No obstante, midiendo en base X $\{\ket{+}, \ket{-}\}$ se obtienen resultados diferentes. Medir $\ket{+}$ en base X siempre retorna $\ket{+}$, mientras que medir $\ket{i}$ en esta base devuelve $\ket{+}$ o $\ket{-}$ con una probabilidad $50:50$.

Normalización

Se dice que un estado cuántico se encuentra normalizado si su probabilidad total es 1, como debería ser. A veces, debe encontrarse una constante de normalización para asegurarse de que esto se cumpla. Por ejemplo, un cubit se encuentra en el estado

$$A = (\sqrt{2}\ket{0} + i\ket{1})$$

Es posible normalizar este estado encontrando la constante de normalización $A$ que asegura que la probabilidad total sea 1. Por lo tanto,

$$\begin{align} 1&= (A\sqrt{2})(A\sqrt{2})^∗ + (Ai)(Ai)^∗\\ &= 2|A|^2 + |A|^2\\ &= 3|A|^2\\ |A|^2&=\frac{1}{3} \end{align}$$

Dado que la fase global no importa, se puede seleccionar una constante $A$ que sea real. Así,

$$A = \frac{1}{\sqrt{3}}$$

y el estado normalizado resultante es el siguiente:

$$\frac{1}{\sqrt{3}}(\sqrt{2}\ket{0} + i\ket{1})$$

Más información

Bibliografía:

Recomendada

Alternativa

Opcional

Libro

Capítulo 2, Introduction to Classical and Quantum Computing (Thomas G. Wong) [Inglés]

Video

Quantum Computing Course: 1.1 Introduction to the Qubit and Superposition (Quantum Soar) [Inglés]

Video

Quantum Computing Course: 1.2 Introduction to Dirac Notation (Quantum Soar) [Inglés]

Video

Quantum Computing Course: 1.3 Representing a Qubit on the Bloch Sphere (Quantum Soar) [Inglés]

Video

Quantum Computing Course: 1.5 Introduction to Phase (Quantum Soar) [Inglés]

Video

Single Systems | Understanding Quantum Information & Computation - Lesson 01 (Qiskit) [Inglés]

Libro

Capítulo 2, Programming Quantum Computers: Essential Algorithms and Code Samples (O'Reilly Media) [Inglés]

Libro

Capítulo 1.2, Quantum Computation and Quantum Information (Michael A. Nielsen; Isaac L. Chuang) [Inglés]

Otros

Global Phase and Relative phase (juweria) [Inglés]

Otros

Explore quantum - Quantum circuits (Microsoft) [Inglés]